聚类
K-means
我们的问题为:
$$
\min _{C_{1}, \ldots, C_{K}} \sum_{k=1}^{K} W\left(C_{k}\right)
$$
$$
W\left(C_{k}\right)=\frac{1}{\left|C_{k}\right|} \sum_{i, j \in C_{k}}\Vert x_{i}-x_{j}\Vert _{2}^{2}
$$
将以上两个式子结合一下,可以得到最优化问题为:
$$
\min _{C_{1}, \ldots, C_{K}} \sum_{k=1}^{K} \frac{1}{\left|C_{k}\right|} \sum_{i, j \in C_{k}}\Vert x_{i}-x_{j}\Vert _{2}^{2}
$$
Centroid
让 \(\mu_{k}=\frac{1}{\left|C_{k}\right|} \sum_{i \in C_{k}} x_{i}\) 为 \( C_{k}\) 的 mean/centroid。
$$
\frac{1}{\left|C_{k}\right|} \sum_{i, j \in \mathcal{C}_{k}}\Vert x_{i}-x_{j}\Vert _{2}^{2}=2 \sum_{i \in C_{k}}\Vert x_{i}-\mu_{k}\Vert _{2}^{2}
$$
代入回之前的式子,优化问题等同于:
$$
\min _{C_{1}, \ldots, C_{K}} \sum_{k=1}^{K}\left\{\sum_{i \in C_{k}}\Vert x_{i}-\mu_{k}\Vert _{2}^{2}\right\}
$$
迭代法
\(\text { binary matrix } R=\left[r_{n k}\right] \in R^{N \times K}
\)
\(\text { 如果 } x_{n} \text { is assigned to cluster } k, \text { 那么 }r_{n k}=1 \text { 并且 } r_{n j}=0, j \neq k\)
**目标:**
找到 \(\left\{\mu_{k}\right\}\),并把每一个数据点分配到一类,使 objective function 最小化。
$$
J\left(R,\left\{\mu_{k}\right\}\right)=\sum_{n=1}^{N}\left[\sum_{k=1}^{K} r_{n k}\Vert x_{n}-\mu_{k}\Vert ^{2}\right]
$$
- \(\mu_{k}=\frac{1}{\left|C_{k}\right|} \sum_{i \in C_{k}} x_{i}\) 为 \( C_{k}\) 的 mean/centroid。
- \(R=\left[r_{n k}\right] \in R^{N \times K}\)
重复以下两步:
- step 1:固定 \(\{\mu_{k}\}\),最优化 \(R\)
- step 2:固定 \(R\),最优化 \(\{\mu_{k}\}\)
具体如下:
step 1
对于某一个具体的 n,我们选择 \(r_{nj}\) 最小化
$$\sum_{k=1}^{K} r_{n k}\Vert x_{n}-\mu_{k}\Vert ^{2}$$
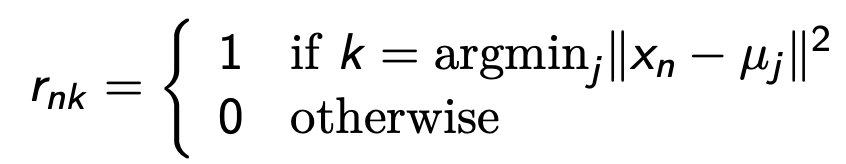
也就是说,将 \(x_n\) 分配给最接近的 centroid。
step 2
对于固定的 \(R\), \(J\left(R,\left\{\mu_{k}\right\}\right)\) 是 convex,quadratic 的,因此,将关于 \(u_{k}\) 的梯度设为 0:
$$
2 \sum_{n=1}^{N} r_{n k}\left(\mu_{k}-x_{n}\right)=0 \Rightarrow \mu_{k}=\frac{\sum_{n=1}^{N} r_{n k} x_{n}}{\sum_{n=1}^{N} r_{n k}}
$$
让 \(u_{k}\) 等于属于 cluster k 的所有数据点 \(x_n\) 的均值

k-means 算法对于异常值十分敏感,因为具有极大值的对象可能会产生严重扭曲的数据分布
k-medoids
k-means 与 k-medoids 之间的差异就是可以理解为对于数据样本的平均值和中位数之间的差异:前者的取值范围可以是连续空间中的任意值,而后者的取值却只能是数据样本范围中的样本。这个原因就是 k-means 对于数据样本的要求太高了,要求所有数据样本处在一个欧式空间中,对于有很多噪声的数据就会造成极大的误差。同时对于非数值型数据样本,不能够计算平均值等实数型变量。
与 K-means 算法类似,区别在于中心点的选取,K-means 中选取的中心点为当前类中所有点的重心,而 K-medoids 法选取的中心点为当前 cluster 中存在的一点,准则函数是当前 cluster 中所有其他点到该中心点的距离之和最小,这就在一定程度上削弱了异常值的影响,但缺点是计算较为复杂,耗费的计算机时间比 K-means 多。
$$
\widehat{J}\left(R,\left\{\mu_{k}\right\}\right)=\sum_{n=1}^{N} \sum_{k=1}^{K} r_{n k} V\left(x_{n}, \mu_{k}\right)
$$
- 其中 \(V\left(x_{n}, \mu_{k}\right)\) 表示 \(x_n\) 和 \(\mu_k\) 的 dissimilarity
Hierarchical Clustering
K-means 需要提前确定 k 的值,而 Hierarchical Clustering 不需要
假设有N个待聚类的样本,对于层次聚类来说,其步骤为:
- 初始化:把每个样本各自归为一类(每个样本自成一类),计算每两个类之间的距离,在这里也就是样本与样本之间的相似度(本质还是计算类与类之间的距离)。
- 寻找各个类之间最近的两个类,把它们归为一类(这样,类的总数就减少了一个)
- 重新计算新生成的这个类与各个旧类之间的距离(相似度)
- 重复 2、3 步,直到所有的样本都归为一类,结束。
2、详细描述:
整个聚类过程其实是建立了一棵树,在建立过程中,可以通过第二步上设置一个阈值,当最近的两个类的距离大于这个阈值,则认为迭代终止。
另外,关键的一步是第三步,如何判断两个类之间的相似度有不少种方法,下面介绍三种:
Single Linkage:又叫做 nearest-neighbor,就是取两个类中最近的两个样本之间的距离作为两个集合的距离,即:最近的两个样本之间的距离越小,
这两个类之间相似度越大,容易造成一种叫做 Chaining 的效果,两个类明明从“大局”上离的比较远,但由于其中个别点距离比较近就被合并了。
这种合并之后 Chaining 效应会进一步扩大,最后得到比较松散的聚类 cluster。
Complete Linkage:完全是 Single Linkage 的反面极端,取两个集合距离最远的两个点的距离作为两个集合的距离,其效果也刚好相反,限制非常大。
两个聚类 cluster 即使已经很接近了,但是只要有不配合的带你存在,就顽固到底,老死不相合并,也是不太好的办法,这两种相似度定义方法共同问题就是:
只考虑了某个特有的数据,而没有考虑类数据整体的特点。
Average Linkage:这种方法就是把两个集合中的点两两距离全部放在一起求平均值,相应的能得到一点合适的结果。
Average Linkage 的一个变种就是取两两距离的中值,与取平均值相比更加能够解除个别偏离样本对结果的干扰。

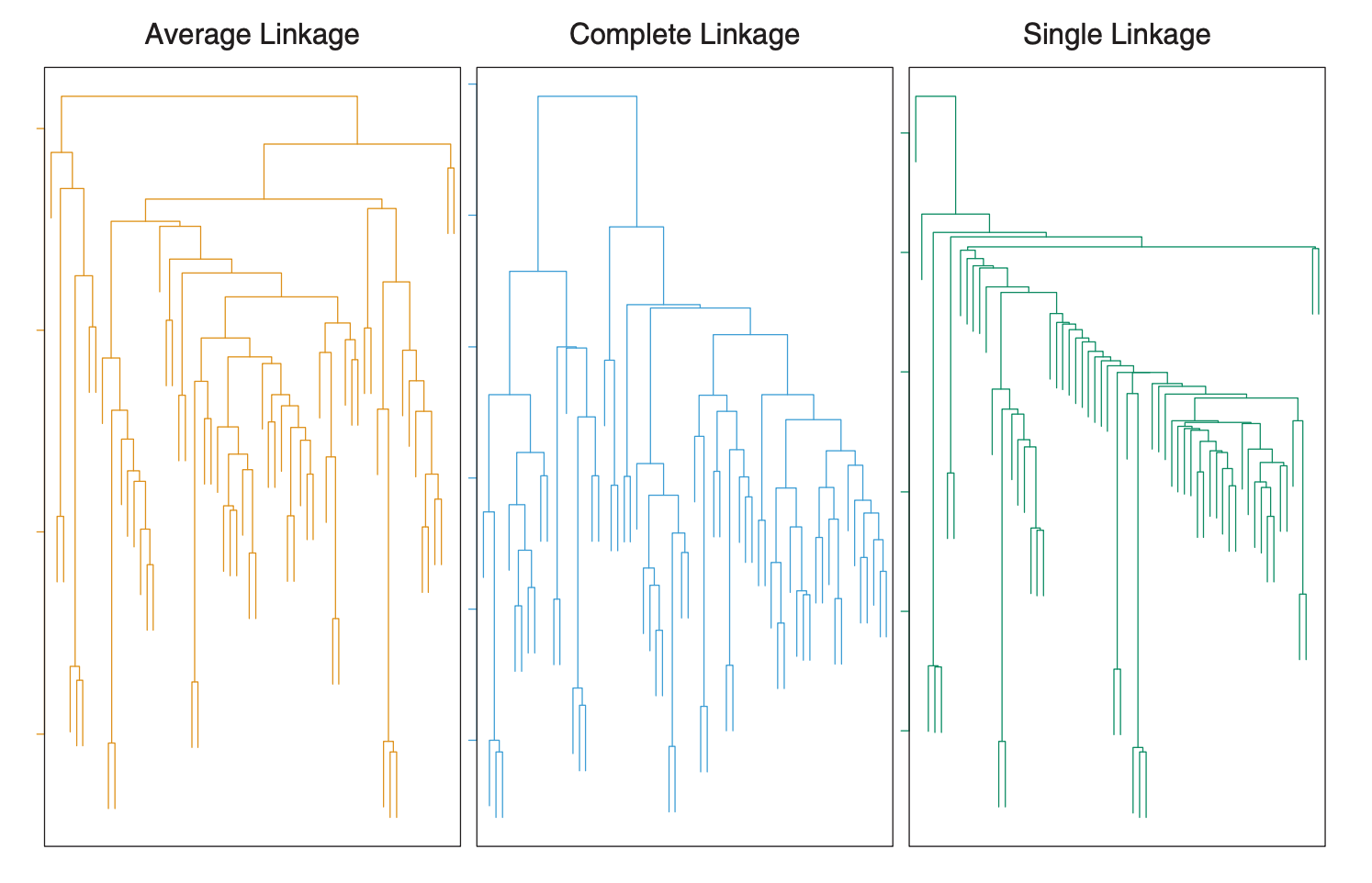
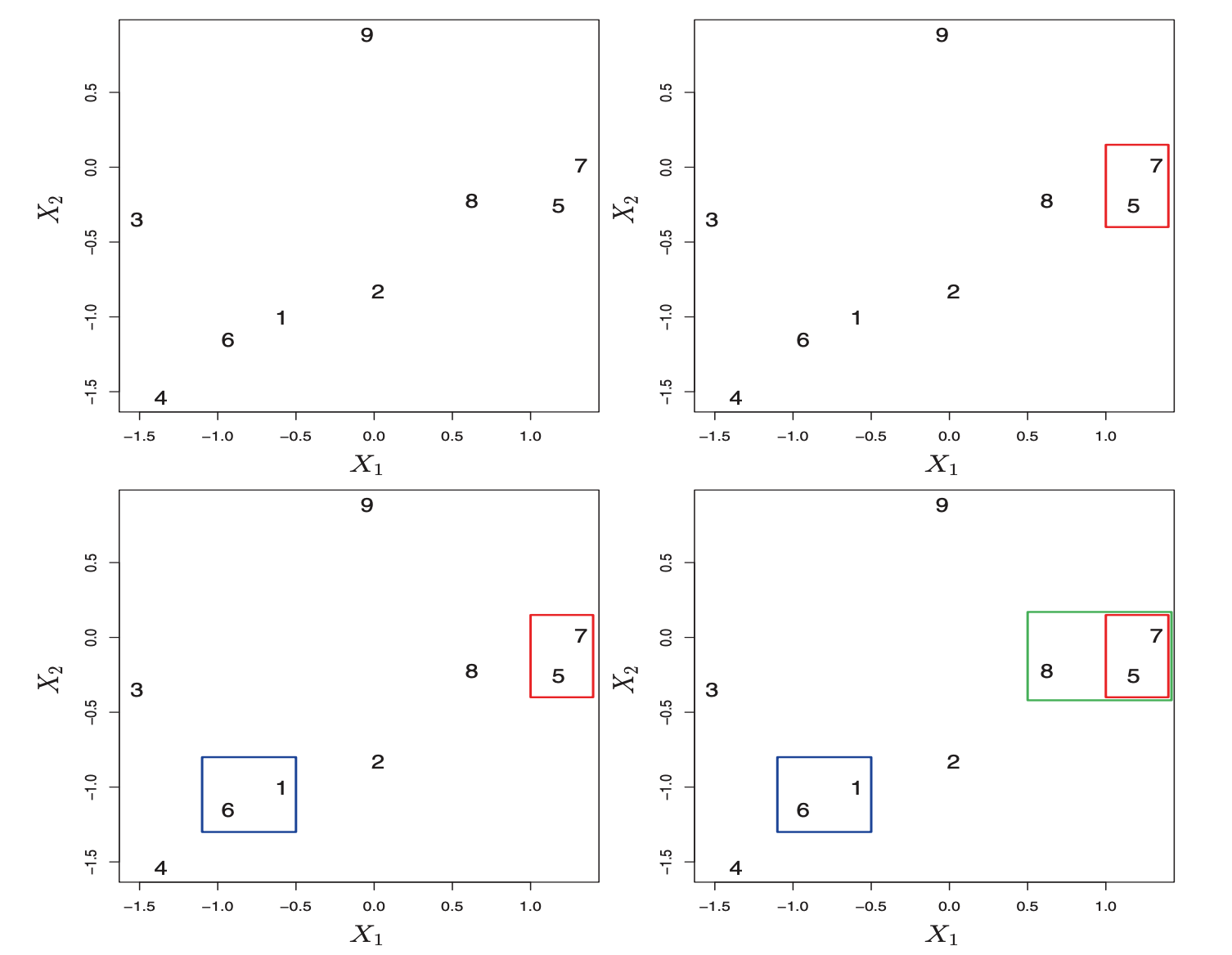
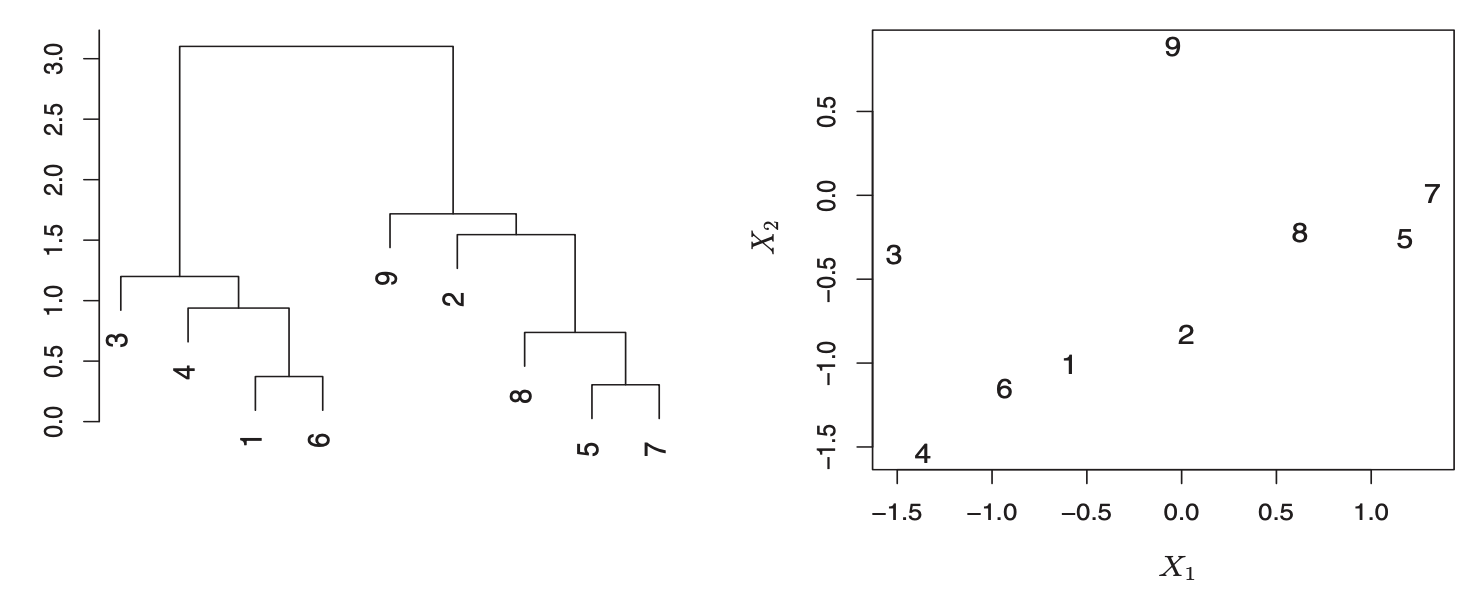

对于 Hierarchical Clustering 的实际应用,有以下问题需要考虑:
- 应该使用哪一种 dissimilarity measure?
- 应该使用哪一种 linkage?
- 什么时候应该切断树状结构?