主成分分析
PCA的思想就是将n维特征映射到k维上(k<n),这k维是重新构造出来的全新维度特征,而不是简单的从n维特征去除n-k维特征,这k维就是主成分。
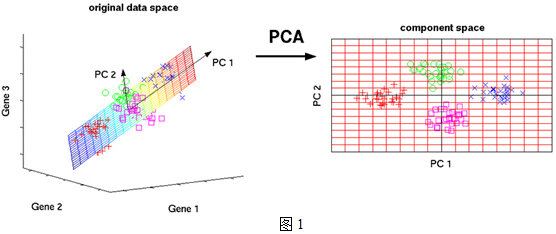
在三维坐标系中,四种颜色的标记界限并不直观,但是在重新定义的二维坐标系中,四种颜色标记界限非常直观,这就是一个典型的PCA,在降维的同时最大程度的保留了数据的特征,为后续的分析提供更直观的支持。
基础数学知识
方差
$$
{Var}(X)=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{2}
$$
协方差
$$
{Cov}(X, Y)=\frac{1}{n} \sum_{i=1}^{n} X_{i} Y_{i}=\frac{1}{n} X \cdot Y
$$
当 \(Cov(a,b)=0\) 时,表示两个字段完全独立,这也是我们的优化目标。
特征值分解
如果说一个向量 \(v\) 是方阵 \(A\) 的特征向量,将一定可以表示成下面的形式:
$$
A v=\lambda v
$$
这时候 \(λ\) 就被称为特征向量 \(v\) 对应的特征值。
一个矩阵的一组特征向量是一组正交向量。
特征分解:
$$
A=Q \Sigma Q^{-1}
$$
其中 \(Q\) 是这个矩阵 \(A\) 的特征向量组成的矩阵,正交矩阵是可逆的。
\(\Sigma=diag\left(\lambda_{1}, \lambda_{2}, \dots, \lambda_{n}\right)\) 是一个对角阵,每一个对角线上的元素就是一个特征值。
一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。
特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么
奇异值分解
特征值分解是一个提取矩阵特征很不错的方法,但是它只适用于方阵。而在现实的世界中,我们看到的大部分矩阵都不是方阵,而奇异值分解是一个能适用于任意的矩阵的一种分解的方法。
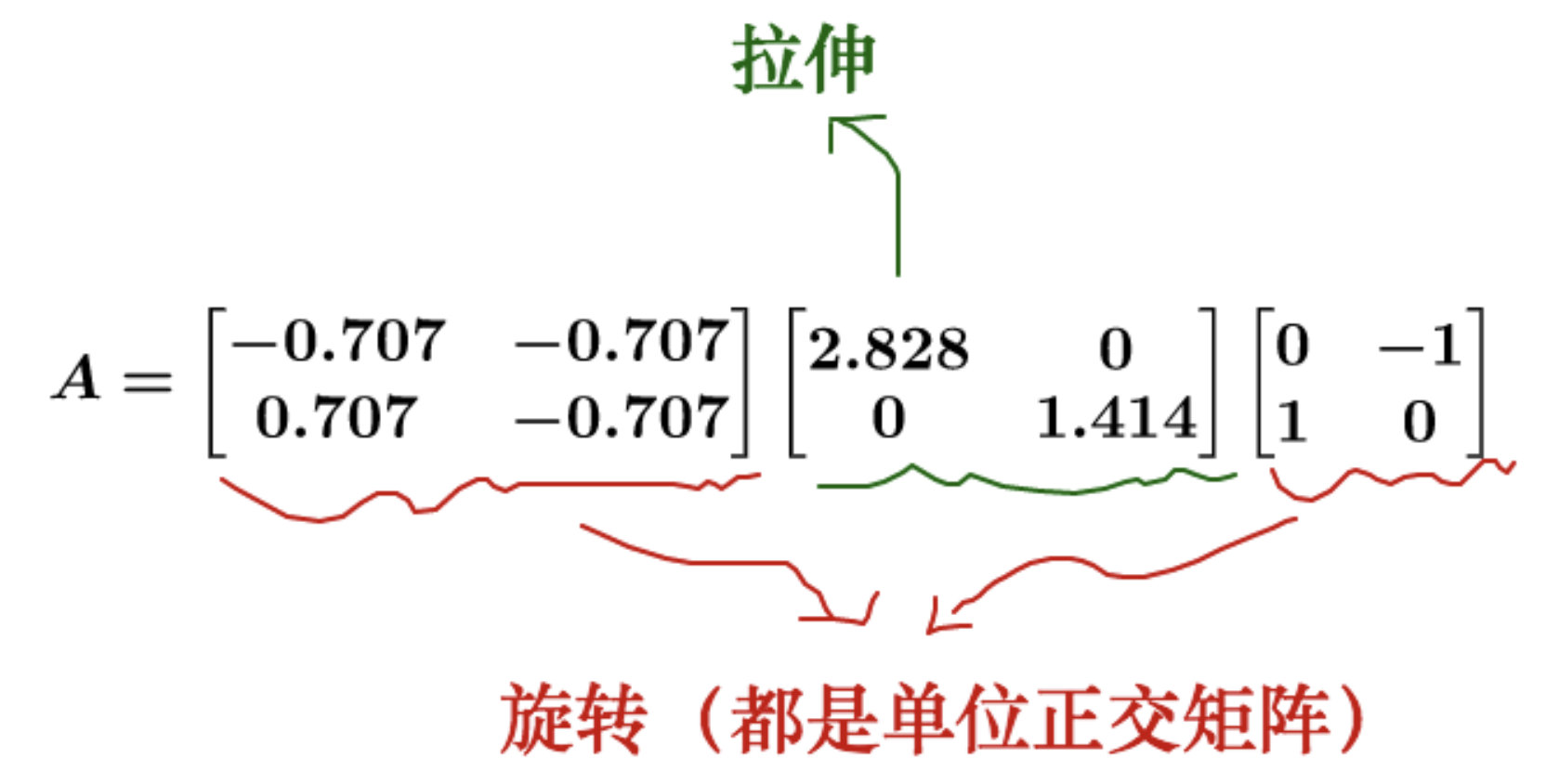
奇异值分解实际上把矩阵的变换分为了三部分:
- 旋转
- 拉伸
- 投影
$$
A=U \Sigma V^{T}
$$
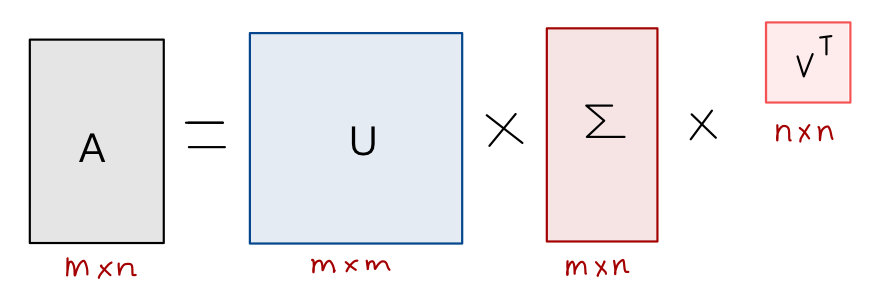
- \(A\) 是一个 \(M * N\) 的矩阵
- \(U\) 是一个 \(M * M\) 的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),
- \(Σ\) 是一个 \(M * N\) 的实数对角矩阵(对角线以外的元素都是 \(0\) ,对角线上的元素称为奇异值),
- \(V^{T}\) 是一个 \(N * N\) 的矩阵,里面的向量也是正交的, \(V\) 里面的向量称为右奇异向量)
奇异值和特征值是怎么对应起来的呢?
首先,我们将一个矩阵A的转置 \(\mathrm{A}^{\top} * \mathrm{A}\),将会得到 \(\mathrm{A}^{\top} \mathrm{A}\) 是一个方阵,我们用这个方阵求特征值可以得到:
$$
\left(A^{T} A\right) v_{i}=\lambda_{i} v_{i}
$$
并且有:
$$
\sigma_{i}=\sqrt{\lambda_{i}}
$$
$$
u_{i}=\frac{1}{\sigma_{i}} A v_{i}
$$
- \(σ_i\) 是就是奇异值,
- \(u_i\) 是左奇异向量
- \(v\) 是右奇异向量
常见的做法是将奇异值由大而小排列。如此 \(Σ\) 便能由 \(M\) 唯一确定。
$$
A=U \Sigma V^{T} \Rightarrow A V=U \Sigma V^{T} V \Rightarrow A V=U \Sigma \Rightarrow A v_{i}=\sigma_{i} u_{i} \Rightarrow \sigma_{i}=A v_{i} / u_{i}
$$
奇异值 \(σ\) 跟特征值类似,在矩阵 \(Σ\) 中也是从大到小排列,而且 \(σ\) 的减少特别的快,在很多情况下,前 10% 甚至 1% 的奇异值的和就占了全部的奇异值之和的 99% 以上了。
也就是说,我们也可以用前 \(r\) 大的奇异值来近似描述矩阵
部分奇异值分解:
$$
A_{m \times n} \approx U_{m \times r} \Sigma_{r \times r} V_{r \times n}^{T}
$$
\(r\) 是一个远小于 \(m\)、 \(n\) 的数,这样矩阵的乘法看起来像是下面的样子:
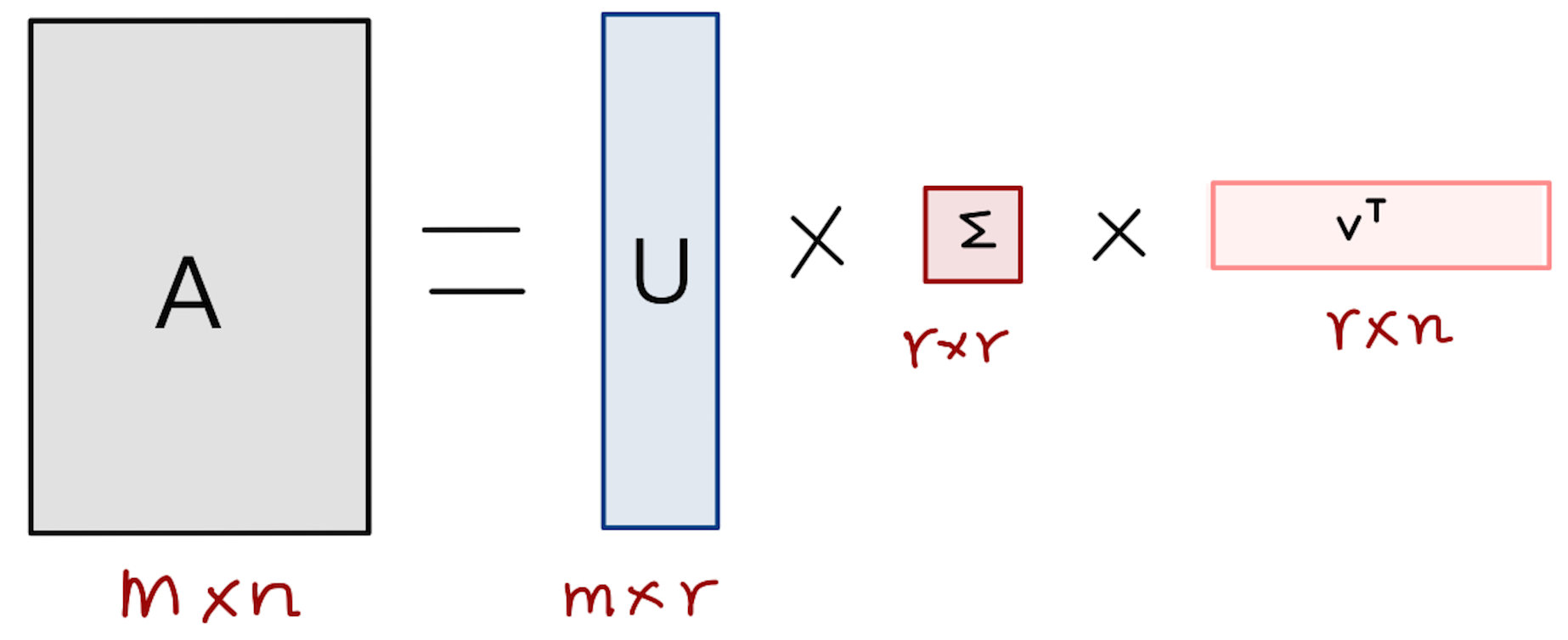
右边的三个矩阵相乘的结果将会是一个接近于 \(A\) 的矩阵,在这儿, \(r\) 越接近于 \(n\) ,则相乘的结果越接近于 \(A\) 。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵 \(A\)。
如果想要压缩空间来表示原矩阵 \(A\),只需存下三个矩阵:\(U、Σ、V\)。