树

二叉树 Binary tree

If every non-leaf node in a binary tree has nonempty left and right subtrees, the tree is termed a strictly binary tree. Or, to put it another way, all of the nodes in a strictly binary tree are of degree zero or two, never degree one.

  • 严格二叉树 Strictly binary tree (full binary tree)
1
2
3
4
5
    18
  /     \   
15       30    
        /  \     
       40   50
  • 完整二叉树 Complete binary tree

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

1
2
3
4
5
        18
     /      \   
   15       30    
  /  \     /      
40    50  100

二叉树遍历：

  • 前序遍历 preorder：先访问根节点 —— 前序遍历左子树 —— 前序遍历右子树 （中左右）
  • 中序遍历 inorder：先访问左子树 —— 根节点 —— 右子树（左中右）
  • 后序遍历 postorder：先访问树的左子树 —— 右子树 —— 根节点（左右中）

二叉树的四种遍历方法笔记

同样的遍历序列可能对应多棵不同的树

二叉搜索树 Binary Search Tree (BST)

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

搜索平均时间: Θ(logn)：The expected height of the tree is logn

最坏情况: Θ(n)：The tree is a linear chain of n nodes

Operations Time
SEARCH O(h)
PREDECESSOR O(h)
SUCCESOR O(h)
MINIMUM O(h)
MAXIMUM O(h)
INSERT O(h)
DELETE O(h)

h 是树的高度，因此，树越高，操作时间越长；树越矮，操作时间越短。

红黑树

属性：

  1. 节点是红色或黑色。
  2. 根节点是黑色。
  3. 每个叶子节点都是黑色的空节点（NIL节点）。
  4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
  5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
  6. (是二叉搜索树)

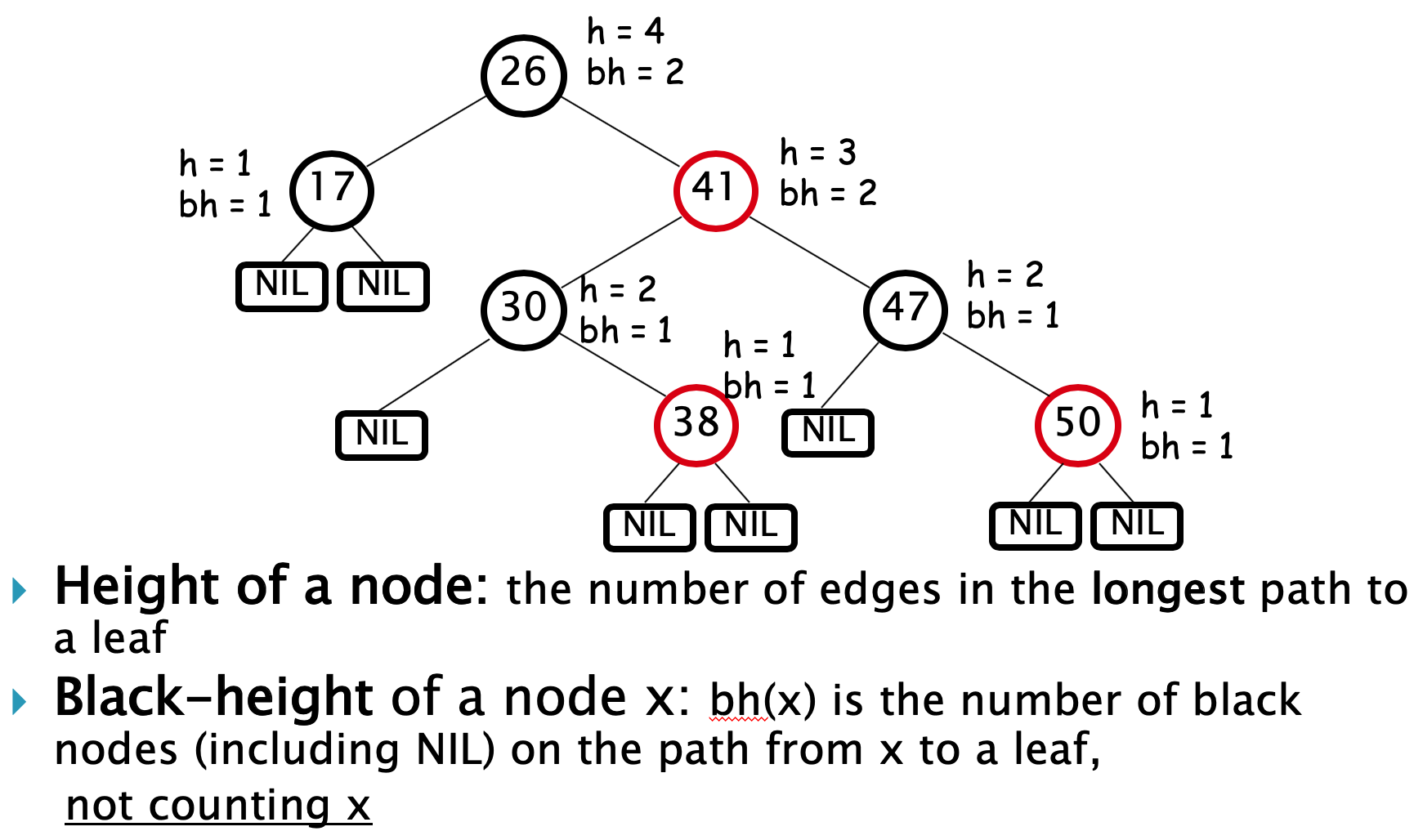
性质：

  • n 个 node 的红黑树的高度最大为 2log(n + 1)
    • 任何 node x 的高度 h(x) 有：bh(x) ≥ h(x)/2
    • 以 x 为 root 的子树包含至少 2^(bh(x)) - 1 个内部 node
  • 从根到叶子的最长路径不会超过最短路径的 2 倍

操作时间复杂度

Operations Time
SEARCH O(logn)
PREDECESSOR O(logn)
SUCCESOR O(logn)
MINIMUM O(logn)
MAXIMUM O(logn)
INSERT O(logn)
DELETE O(logn)

左旋与右旋

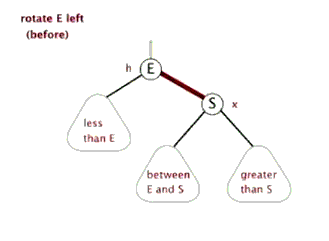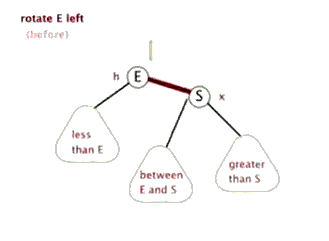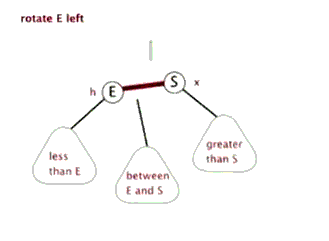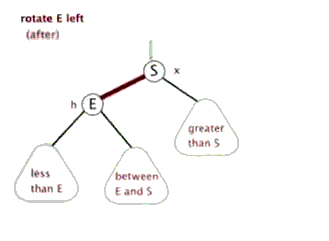
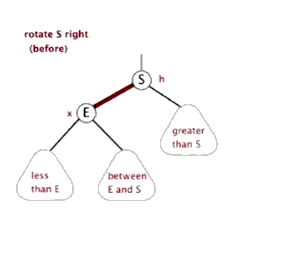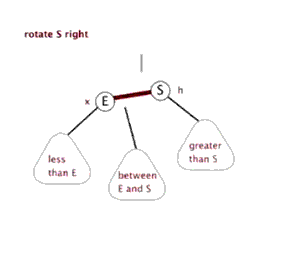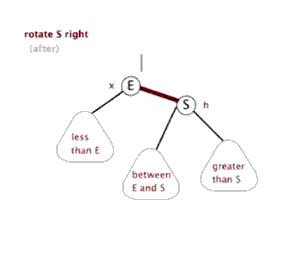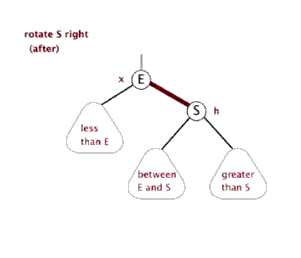
AVL 树

属性：

  1. （是二叉搜索树）
  2. 每个节点的左子树和右子树的高度差最多为 1

红黑树 Vs AVL树

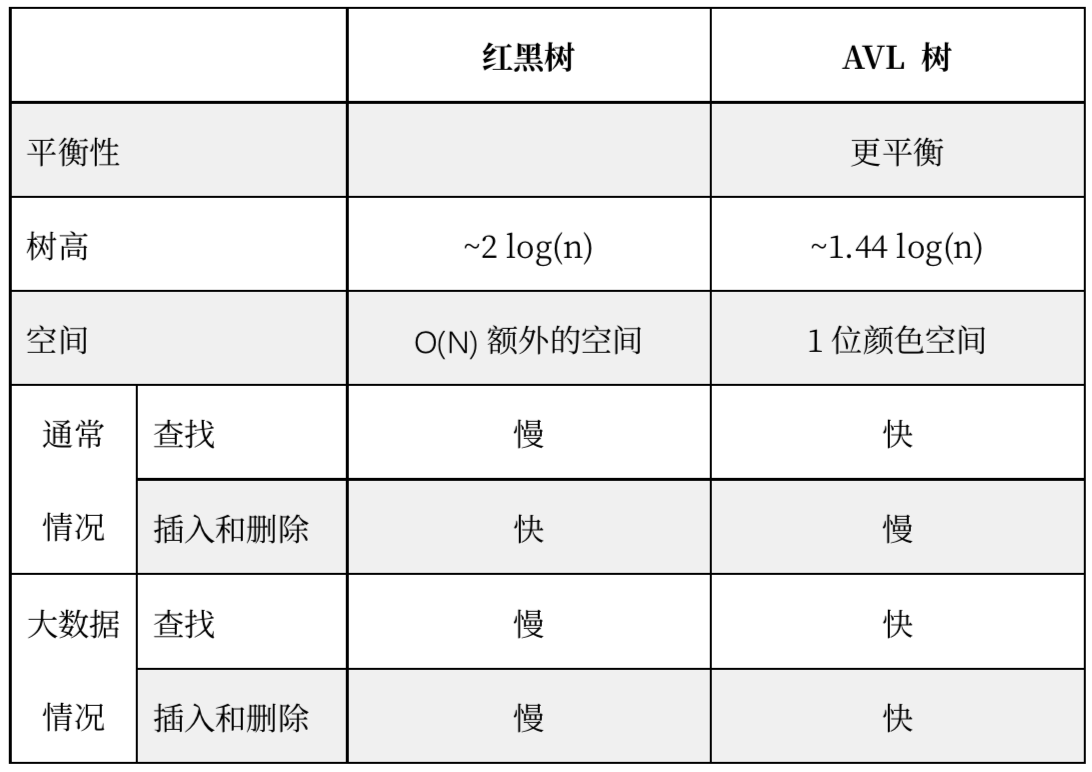
  • AVL 树中的查找通常更快，但这是以插入和删除速度慢为代价的，因为需要更多的旋转操作。因此，如果您希望查找的重要性大于的更新的重要性，则使用AVL树。
  • 在大多数语言库中都使用红黑树，如 C++ 中的 map、MultIAP、MultiSet 等，而 AVL 树则用于数据库中，因为需要更快的检索。
  • 大数据的情况，因为在插入之前需要查找特定节点。AVL 树和 RB 树在最坏的情况下仍然只需要固定的旋转次数。因此，瓶颈是查找该特定节。

B 树

为什么需要 B 树？

磁盘IO与预读

磁盘读取依靠的是机械运动，分为寻道时间、旋转延迟、传输时间三个部分，这三个部分耗时相加就是一次磁盘IO的时间，大概9ms左右（需要等待一个磁盘转完完整的一圈）。这个成本是访问内存的十万倍左右；正是由于磁盘IO是非常昂贵的操作，所以计算机操作系统对此做了优化：预读；每一次IO时，不仅仅把当前磁盘地址的数据加载到内存，同时也把相邻数据也加载到内存缓冲区中。因为局部预读原理说明：当访问一个地址数据的时候，与其相邻的数据很快也会被访问到。每次磁盘IO读取的数据我们称之为一页（page）。一页的大小与操作系统有关，一般为4k或者8k。这也就意味着读取一页内数据的时候，实际上发生了一次磁盘IO。

当搜索表保存在磁盘上时，每次磁盘传输的成本很高，但并不很大程度上取决于传输的数据量，特别是如果传输的是连续的项目。

B-Tree与二叉查找树的对比

我们知道二叉查找树查询的时间复杂度是O（logN），查找速度最快和比较次数最少，既然性能已经如此优秀，但为什么实现索引是使用B-Tree而不是二叉查找树，关键因素是磁盘IO的次数。

数据库索引是存储在磁盘上，当表中的数据量比较大时，索引的大小也跟着增长，达到几个G甚至更多。当我们利用索引进行查询的时候，不可能把索引全部加载到内存中，只能逐一加载每个磁盘页，这里的磁盘页就对应索引树的节点。

二叉树

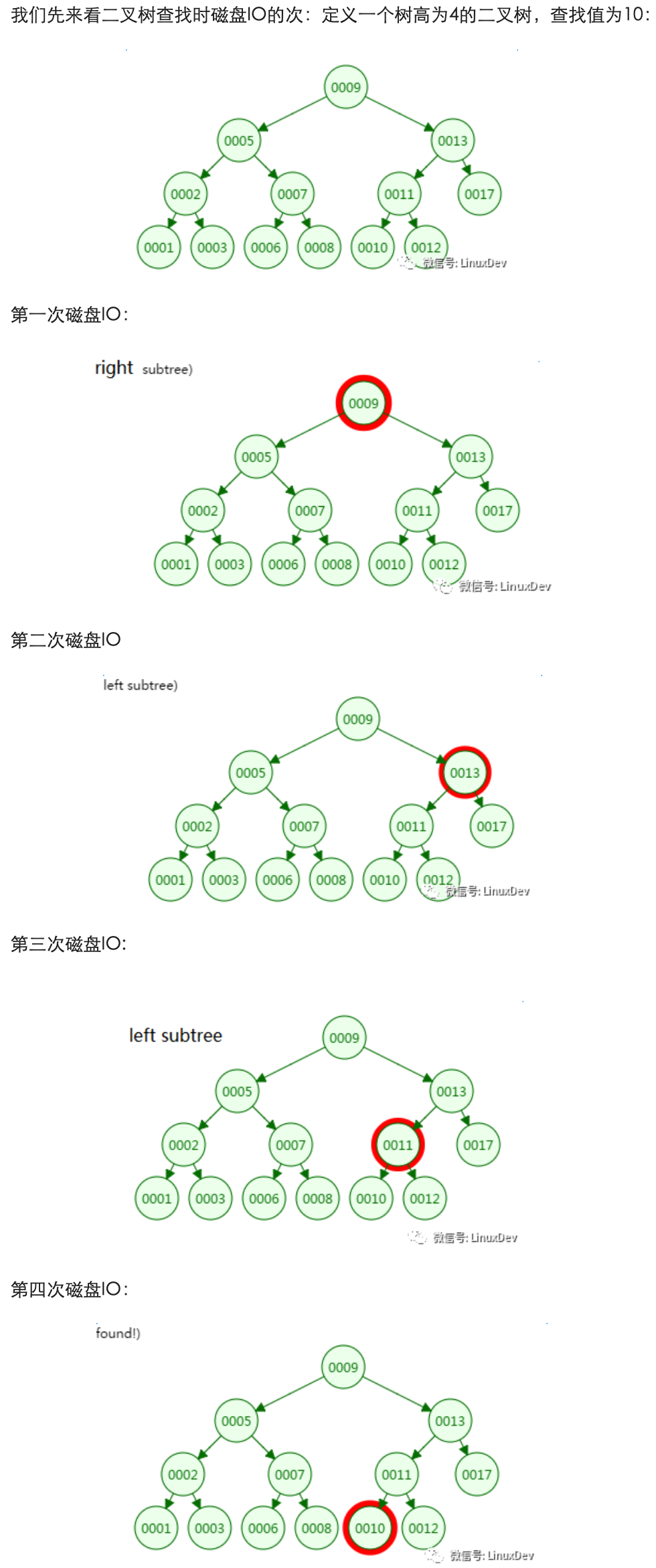
从二叉树的查找过程了来看，树的高度和磁盘IO的次数都是4，所以最坏的情况下磁盘IO的次数由树的高度来决定。

从前面分析情况来看，减少磁盘IO的次数就必须要压缩树的高度，让瘦高的树尽量变成矮胖的树，所以B-Tree就在这样伟大的时代背景下诞生了。

B-Tree

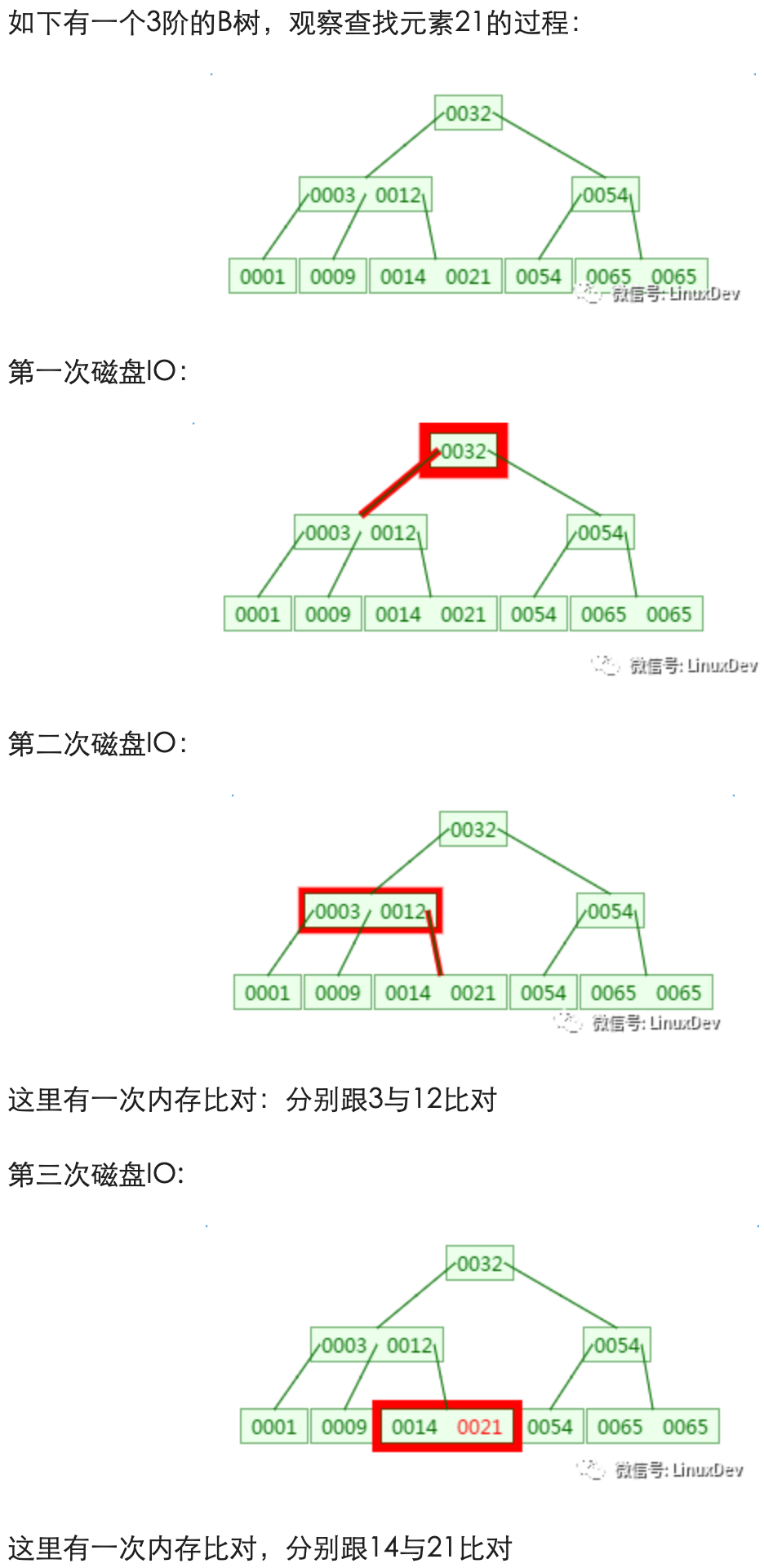
从查找过程中发现，B树的比对次数和磁盘IO的次数与二叉树相差不了多少，所以这样看来并没有什么优势。

但是仔细一看会发现，比对是在内存中完成中，不涉及到磁盘IO，耗时可以忽略不计。另外B树种一个节点中可以存放很多的key（个数由树阶决定）。

相同数量的key在B树中生成的节点要远远少于二叉树中的节点，相差的节点数量就等同于磁盘IO的次数。这样到达一定数量后，性能的差异就显现出来了。

B树主要应用于文件系统以及部分数据库索引，如MongoDB，大部分关系型数据库索引则是使用B+树实现。

规则：

  1. 排序方式：所有节点关键字是按递增次序排列，并遵循左小右大原则；
  2. 非叶节点的 key 数比它的子树的数量小 1；
  3. 子节点数：非叶节点（除了 root）的子节点数为，[ceil(M/2), M]；root 要么是一个叶节点，要么有 [2, m] 个子节点；
  4. key 数：除了 root 所有 node 的 key 数量为 [ceil(M/2) - 1, M-1]；
  5. 所有叶子节点均在同一层，叶节点包含不超过 M - 1 个 key。

B-tree of order 4：

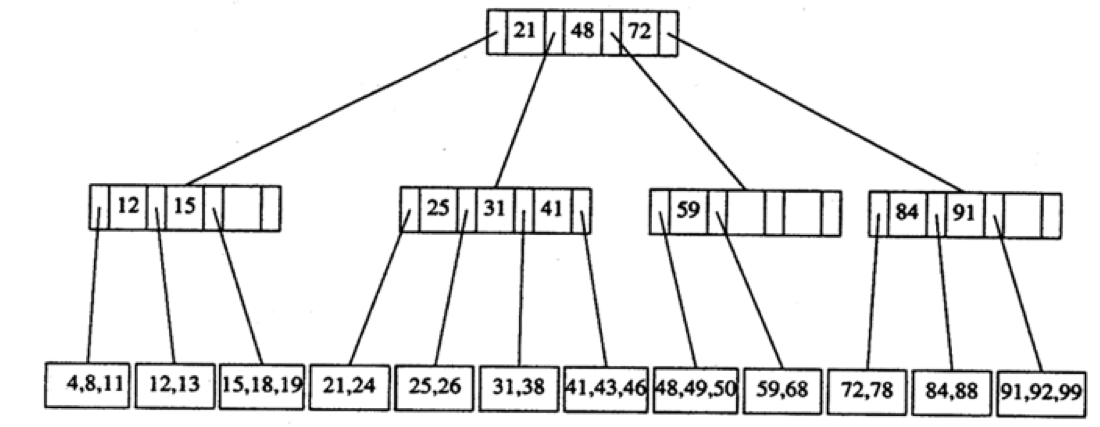
图

入度 in-degree：进入该节点的边的条数
出度 out-degree：从该节点出发的边的条数

连通图

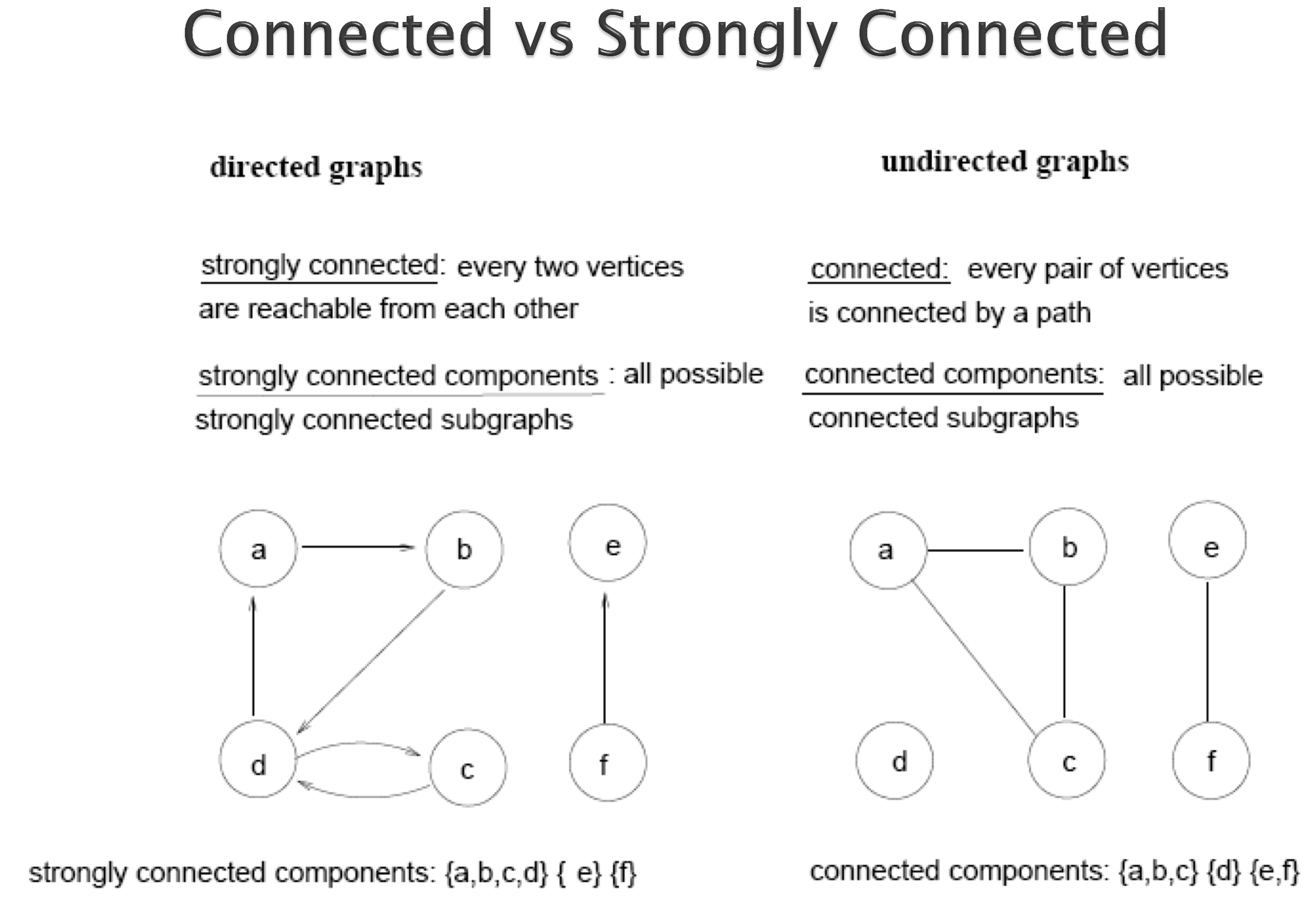
A tree is a connected, acyclic “undirected” graph

邻接表与邻接矩阵

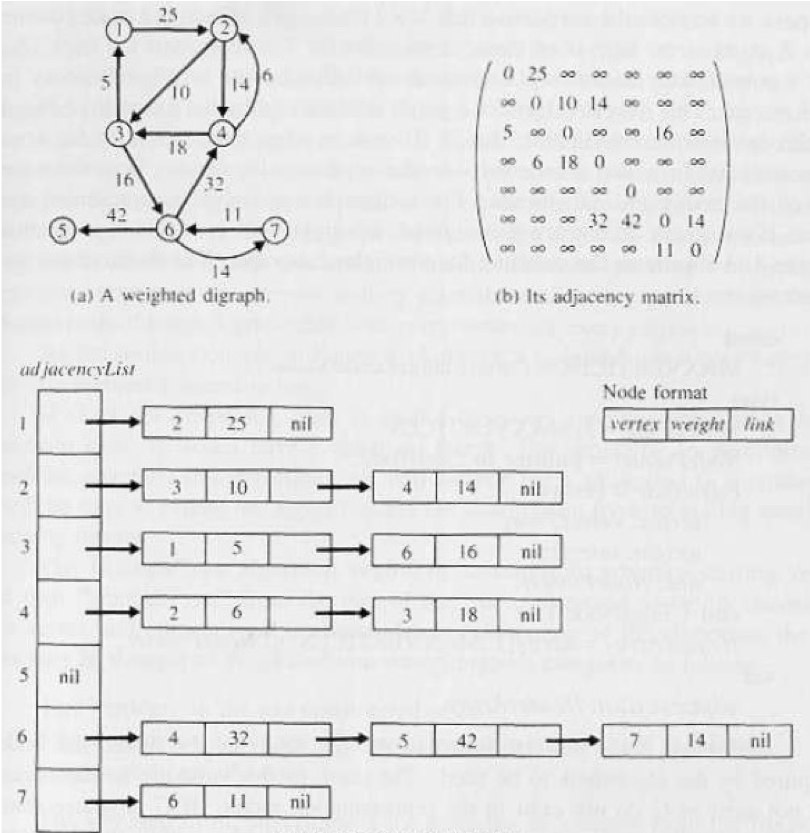
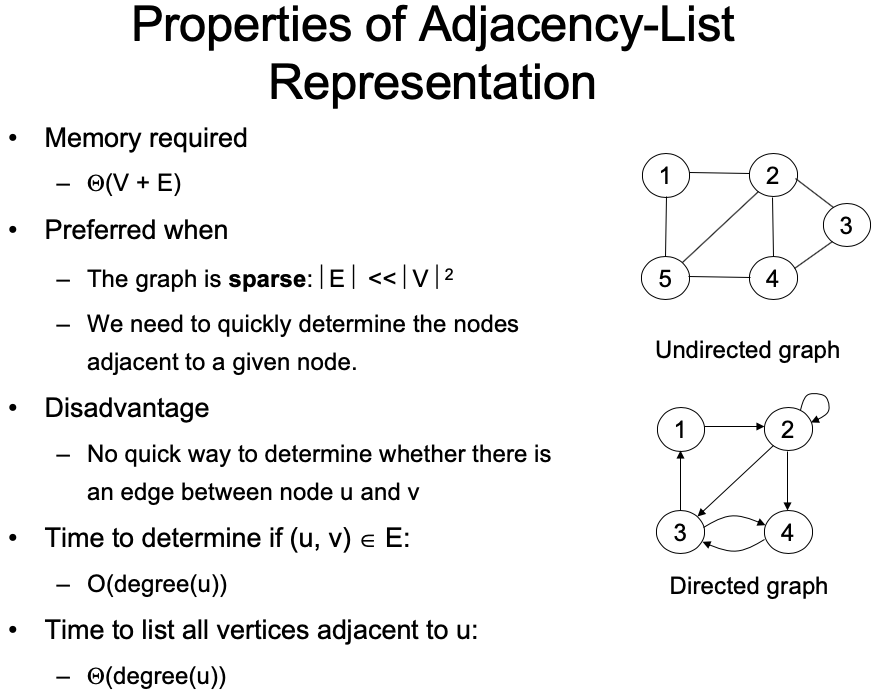
拓扑排序 Topological sort

有向无环图（DAG）至少有一种拓扑排序，非 DAG 图没有拓扑排序。

当有向无环图满足以下条件时：

  1. 每一个顶点出现且只出现一次
  2. 若A在序列中排在B的前面，则在图中不存在从B到A的路径。

我们称这样的图，是一个拓扑排序的图。
与之前的树结构对比不难发现，树结构其实可以转化为拓扑排序，而拓扑排序 不一定能够转化为树。

算法：

  1. 根据邻接矩阵或邻接表计算入度数组
  2. 取入度为 0 的 vertex
  3. 打印该 vertex，并移除它，和它的 edge
  4. 判断减小后是否有新的入度为 0 的 vertex，继续进行第2步
  5. 直到所有 vertex 入度为 0、得到拓扑排序序列，或返回失败

Running time is O(|V|^2).

1
2
3
4
5
6
7
8
9
10
11
void topsort () {  
	for (int counter=0; counter<numVertex; counter++) {
		Vertex v = FindNewVertexOfInDegreeZero (); //check all vertices
		if (v == null) {
			Error(“Cycle Found”); return;
		}
		v.topNum = counter;
		for each Vertex w adjacent to v
			w.indegree--;
	}
}

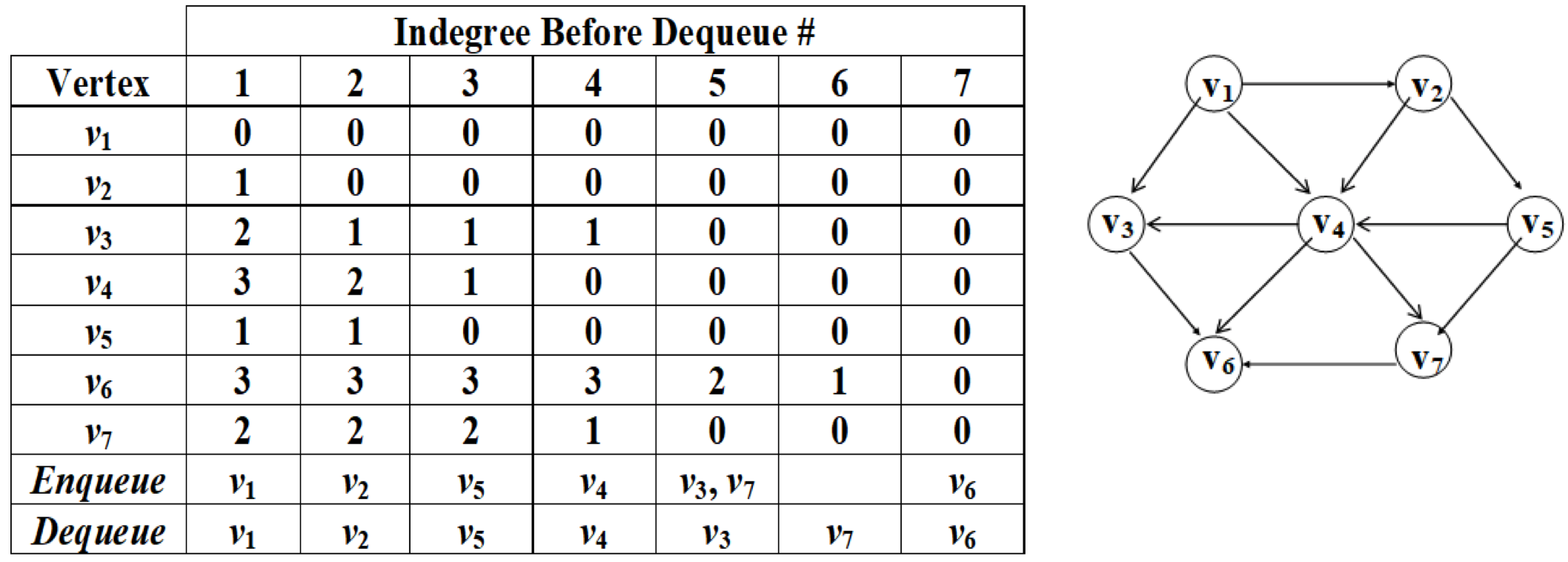
改进版本：

  1. 将 indegree 0的所有未分配顶点保留在队列中。
  2. 当队列不为空：
    1. 在队列中删除一个顶点。
    2. 减小所有相邻顶点的度数。
    3. 如果相邻顶点的度数变为0，则使该顶点入队。

运行时间为 O(| E | + | V |)。

最短路径

单源点的最短路径问题是指：

给定一个加权有向图 G 和源点 s，对于图 G 中的任意一点 v，求从 s 到 v 的最短路径。

Dijkstra 算法

Bellman-Ford 算法

  • APP: 算法动画图解

两种算法的区别：

bellman-ford

  • bellman-ford的一个优势是可以用来判断是否存在负环

求单源最短路，可以判断有无负权回路（若有，则不存在最短路），时效性较好，时间复杂度O（VE）。Bellman-Ford算法是求解单源最短路径问题的一种算法。

求单源、无负权的最短路。时效性较好，时间复杂度为O（VV+E）。源点可达的话，O（VlgV+ElgV）=>O（ElgV）。

最小生成树

数据结构-图及相关算法

  • MST 不是唯一的
  • MST 没有 cycle
  • MST 的 edge 的数量：|V| - 1

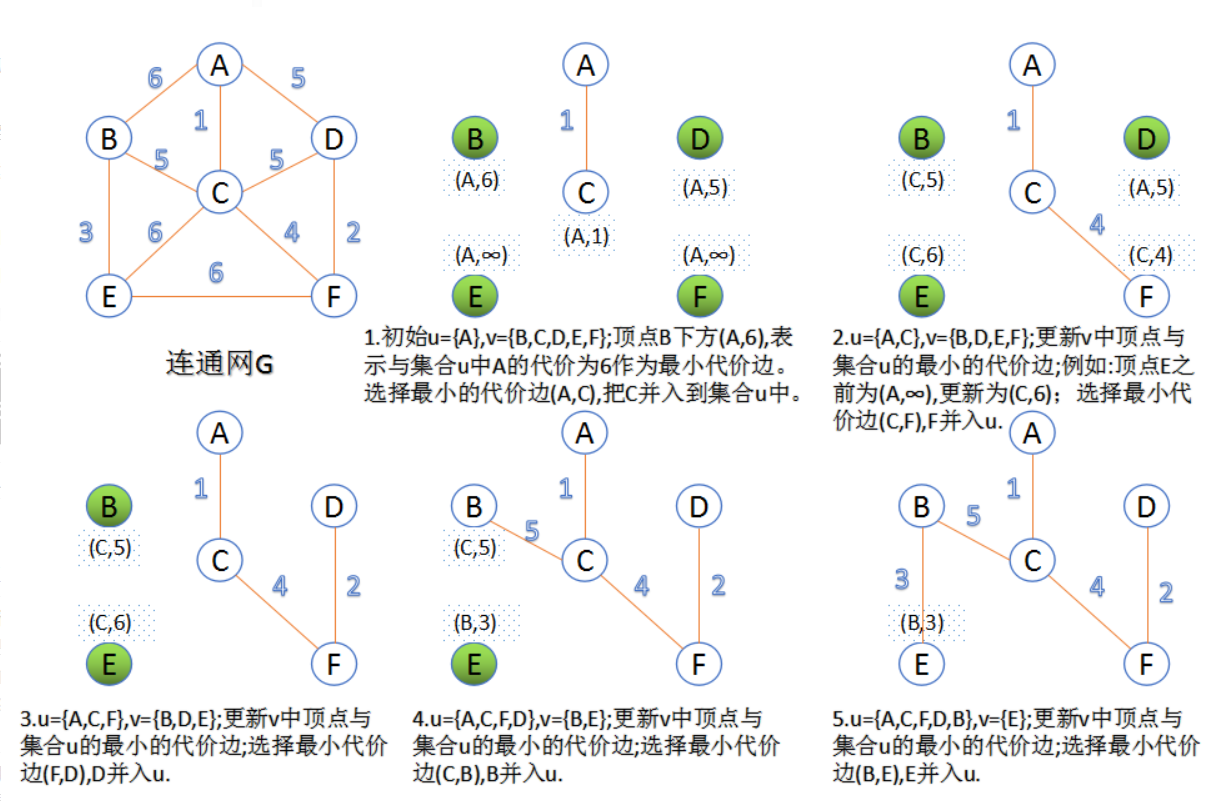
Prim 算法

首先以一个结点作为最小生成树的初始结点，然后以迭代的方式找出与最小生成树中各结点权重最小边，并加入到最小生成树中。加入之后如果产生回路则跳过这条边，选择下一个结点。当所有结点都加入到最小生成树中之后，就找出了连通图中的最小生成树了。

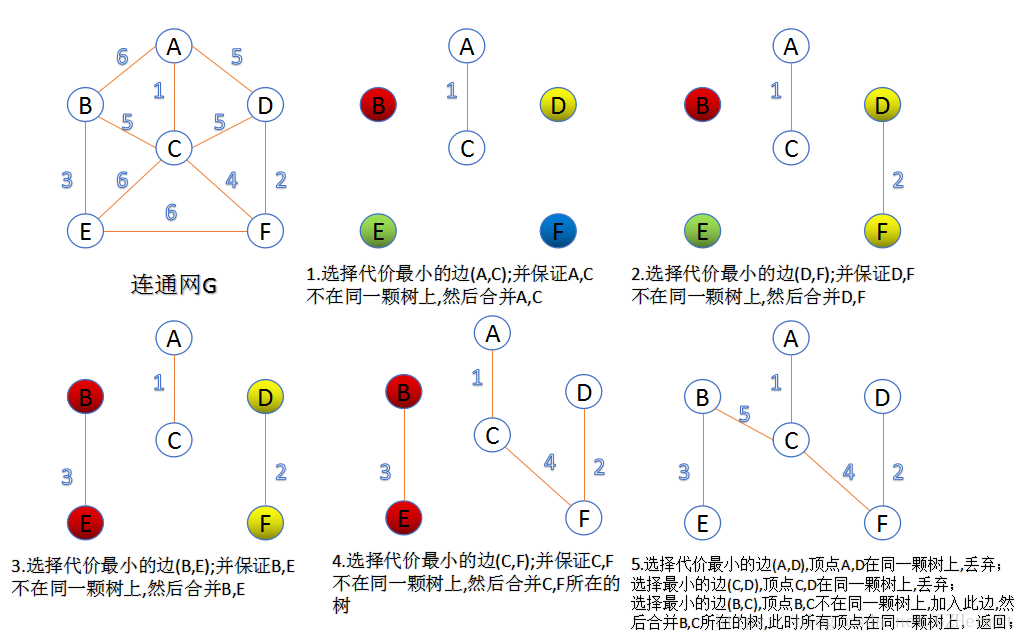
Kruskal 算法

Kruskal算法与Prim算法的不同之处在于，Kruskal在找最小生成树结点之前，需要对所有权重边做从小到大排序。将排序好的权重边依次加入到最小生成树中，如果加入时产生回路就跳过这条边，加入下一条边。当所有结点都加入到最小生成树中之后，就找出了最小生成树。

Prim Vs Kruskal

  • 两者都可以处理负权重
  • One begins with an edge while the other starts with a node.
  • One selects the next edge in order while the other does it from one node to another node.
  • One works on both connected and disconnected graphs while the other is mainly for connected graph.
  • One is good for sparse graph and the other is for dense graph.
    • Depending on the implementation of data structure.

prim: 该算法的时间复杂度为O(n2)。与图中边数无关，该算法适合于稠密图。

kruskal: 需要对图的边进行访问，所以克鲁斯卡尔算法的时间复杂度只和边又关系，可以证明其时间复杂度为O（eloge）。适合稀疏图。

无疑，Kruskal算法在效率上要比Prim算法快，因为Kruskal只需要对权重边做一次排序，而Prim算法则需要做多次排序。尽管Prim算法每次做的算法涉及的权重边不一定会涵盖连通图中的所有边，但是随着所使用的排序算法的效率的提高，Kruskal算法和Prim算法之间的差异将会清晰的显性出来。

时间上：Prim适合稠密图，复杂度为O(n * n)，因此通常使用邻接矩阵储存，复杂度为O(e * loge)，而Kruskal多用邻接表。
稠密图 Prim > Kruskal，稀疏图 Kruskal > Prim。

空间上： Prim适合点少边多，Kruskal适合边多点少。

动态规划

采用动态规划时，并不需要去一一计算那些重叠了的子问题。
或者说：用了动态规划之后，有些子问题 是通过 “查表” 直接得到的，而不是重新又计算一遍得到的。

  1. 最优子结构

    问题的最优解包含子问题的最优解
    从子问题的最优解自下而上建立整个问题的最优解

  2. 重叠子问题

    如果递归算法一遍又一遍地重新访问相同的子问题，则该问题具有重叠的子问题

DP算法的运行时间取决于两个因素：

  • 子问题总数

  • 每个子问题有多少选择

  • Θ(n) 个子问题

  • 每个子问题有 2 个选择
    ————> Θ(n)

  • Θ(n^2) 个子问题

  • 约有 n-1 个选择
    ————> Θ(n^3)

最长公共子序列 LCS

算法设计与分析/动态规划——最长公共子序列LCS及模板