Regression
基础
- null hypothesis (原假设):假设 X 和 Y 并没有关系
- alternative hypothesis (备选假设):假设 X 和 Y 是有关系的
统计量 t 值:
$$
t=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}
$$
回归评价指标
Residual Standard Error
$$
\operatorname{RSE}=\sqrt{\frac{1}{n-2} \operatorname{RSS}}=\sqrt{\frac{1}{n-2} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}
$$
residual sum-of-squares
$$
R S S=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}
$$
R-squared
$$
R^{2}=\frac{\mathrm{TSS}-\mathrm{RSS}}{\mathrm{TSS}}=1-\frac{\mathrm{RSS}}{\mathrm{TSS}} =1-\frac{\sum(y-\hat{y})^{2}}{\sum(y-\overline{y})^{2}}
$$
total sum of squares
$$
\mathrm{TSS}=\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}
$$
在简单线性回归中:
$$
R^{2}=r^{2}
$$
其中 \( r \) 是\( X \) 和\( Y \)的相关系数
$$
r=\frac{\sum_{i=1}^{n}\left(x_{i}-\overline{x}\right)\left(y_{i}-\overline{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\overline{x}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}}}
$$
linear regression
single predictor
假设模型为:
$$
Y=\beta_{0}+\beta_{1} X+\epsilon
$$
- \( \beta_{0} \) 被称为 intercept
- \( \beta_{1} \) 被称为 slope
给出估计值 \( \hat{\beta}_{0} \) 和 \( \hat{\beta}_{1} \),我们预测:
$$
\hat{y}=\hat{\beta}_{0}+\hat{\beta}_{1} x
$$
- hat 符号代表是估计值
使 residual 为:
$$
e_{i}=y_{i}-\hat{y}_{i}
$$
residual sum of squares (RSS) 为:
$$
\mathrm{RSS}=e_{1}^{2}+e_{2}^{2}+\cdots+e_{n}^{2}
$$
等同于:
$$
\mathrm{RSS}=\left(y_{1}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{1}\right)^{2}+\left(y_{2}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{2}\right)^{2}+\ldots+\left(y_{n}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{n}\right)^{2}
$$
为了最小化 RSS,我们得到:
$$
\hat{\beta}_{1}=\frac{\sum_{i=1}^{n}\left(x_{i}-\overline{x}\right)\left(y_{i}-\overline{y}\right)}{\sum_{i=1}^{n}\left(x_{i}-\overline{x}\right)^{2}}
$$
$$
\hat{\beta}_{0}=\overline{y}-\hat{\beta}_{1} \overline{x}
$$
$$
\begin{array}{l}{\text { where } \overline{y} \equiv \frac{1}{n} \sum_{i=1}^{n} y_{i} \text { and } \overline{x} \equiv \frac{1}{n} \sum_{i=1}^{n} x_{i} \text { are the sample }} \ {\text { means. }}\end{array}
$$
Multiple Linear Regression
模型为:
$$
Y=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{p} X_{p}+\epsilon
$$
给出估计值 \( \hat{\beta}_{0}, \hat{\beta}_{1}, \ldots \hat{\beta}_{p} \) 我们预测:
$$
\hat{y}=\hat{\beta}_{0}+\hat{\beta}_{1} x_{1}+\hat{\beta}_{2} x_{2}+\cdots+\hat{\beta}_{p} x_{p}
$$
$$
\mathrm{RSS}=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}
$$
$$
=\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{i 1}-\hat{\beta}_{2} x_{i 2}-\cdots-\hat{\beta}_{p} x_{i p}\right)^{2}
$$
最小化 RSS 的 \( \hat{\beta}_{0}, \hat{\beta}_{1}, \ldots \hat{\beta}_{p} \) 就是 multiple least squares regression coefficient estimates。
Model selection
Forward selection
- 从一个 null model 开始(一个只有 intercept 没有 predictors 的模型)
Backward selection
- 从包含所有变量的模型开始
- 移除最大 p 值的变量,也就是最小显著性的变量
- 拟合新的 (p-1) 变量的模型,再次移除最大 p 值的变量
- 重复直到满足阈值条件
Logistic Regression
$$
p(X)=\frac{e^{\beta_{0}+\beta_{1} X}}{1+e^{\beta_{0}+\beta_{1} X}}
$$
可以看出不论参数如何变化, \( p(X) \)的值始终在 0 和 1 内
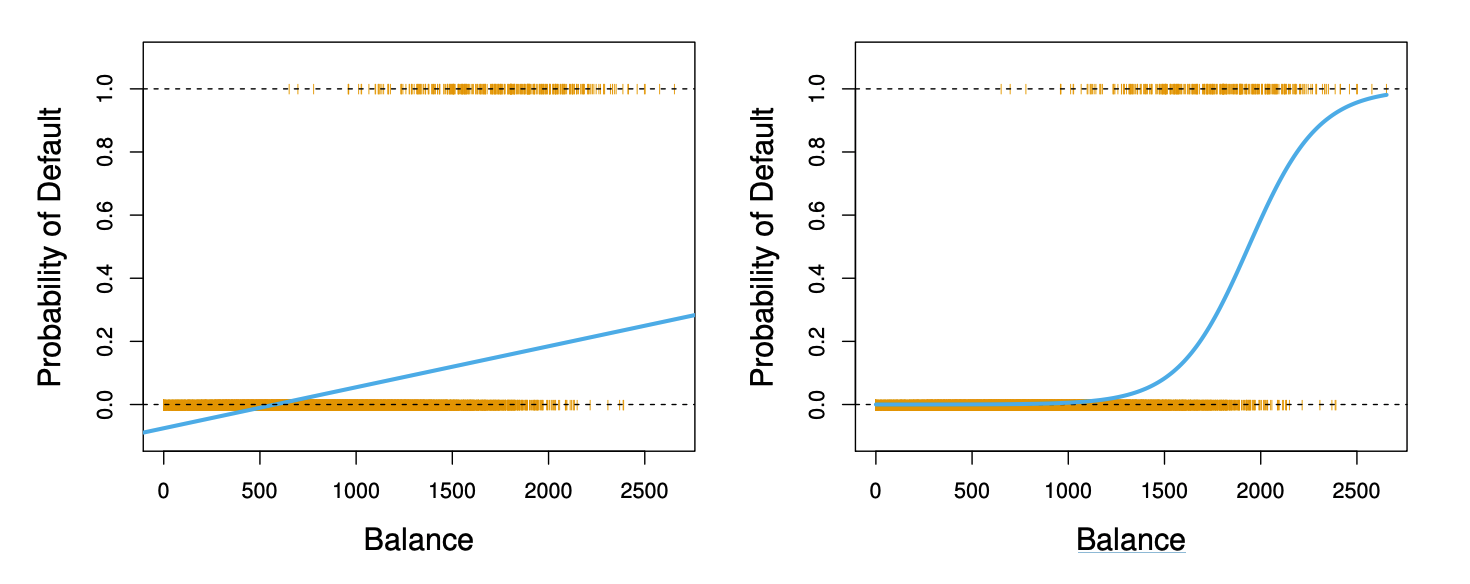
如果进行一点转变,被称为 log odds 或者 logit transformation of \( p(X) \),则有:
$$
\log \left(\frac{p(X)}{1-p(X)}\right)=\beta_{0}+\beta_{1} X
$$
我们使用极大似然来进行参数估计:
$$
\ell\left(\beta_{0}, \beta\right)=\prod_{i : y_{i}=1} p\left(x_{i}\right) \prod_{i : y_{i}=0}\left(1-p\left(x_{i}\right)\right)
$$
对于多个变量:
$$
\log \left(\frac{p(X)}{1-p(X)}\right)=\beta_{0}+\beta_{1} X_{1}+\cdots+\beta_{p} X_{p}
$$
$$
p(X)=\frac{e^{\beta_{0}+\beta_{1} X_{1}+\cdots+\beta_{p} X_{p}}}{1+e^{\beta_{0}+\beta_{1} X_{1}+\cdots+\beta_{p} X_{p}}}
$$
对于多于两个类:
$$
\operatorname{Pr}(Y=k | X)=\frac{e^{\beta_{0 k}+\beta_{1 k} X_{1}+\ldots+\beta_{p k} X_{p}}}{\sum_{\ell=1}^{K} e^{\beta_{0 \ell}+\beta_{1 \ell} X_{1}+\ldots+\beta_{p \ell} X_{p}}}
$$
Discriminant Analysis
用于分类的贝叶斯法则
$$
\operatorname{Pr}(Y=k | X=x)=\frac{\operatorname{Pr}(X=x | Y=k) \cdot \operatorname{Pr}(Y=k)}{\operatorname{Pr}(X=x)}
$$
稍微改变一下用于 discriminant analysis
$$
\operatorname{Pr}(Y=k | X=x)=\frac{\pi_{k} f_{k}(x)}{\sum_{l=1}^{K} \pi_{l} f_{l}(x)}
$$
- \( f_{k}(x)=\operatorname{Pr}(X=x | Y=k) \) 是\( X \)在分类 \( k \)中的 density
- \( \pi_{k}=\operatorname{Pr}(Y=k) \) 是分类\( k \)的marginal 或 prior probability
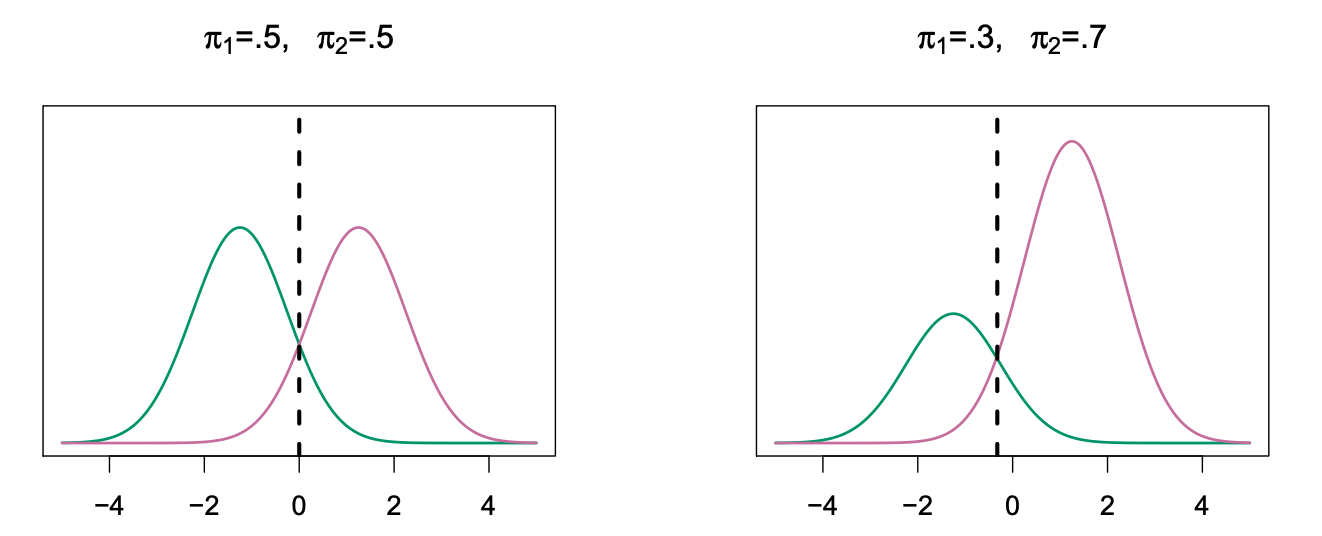
哪一个分类的 density 最高就为哪一个分类
Summary
- Logistic regression is very popular for classification, especially when \( K = 2 \).
- LDA is useful when \( n \) is small, or the classes are well separated, and Gaussian assumptions are reasonable. Also when \( K > 2 \).
- Naive Bayes is useful when \( p \) is very large.