Normalization
Normalization
独立同分布与白化
独立同分布,即 independent and identically distributed,简称为 i.i.d. 独立同分布并非所有机器学习模型的必然要求(比如 Naive Bayes 模型就建立在特征彼此独立的基础之上,而 Logistic Regression 和神经网络则在非独立的特征数据上依然可以训练出很好的模型),但独立同分布的数据可以简化常规机器学习模型的训练、提升机器学习模型的预测能力,已经是一个共识。
因此,在把数据喂给机器学习模型之前,“白化(whitening)”是一个重要的数据预处理步骤。白化一般包含两个目的:
- 去除特征之间的相关性 \(\longrightarrow\) 独立;
- 使得所有特征具有相同的均值和方差 \(\longrightarrow\) 同分布。
白化最典型的方法就是PCA,可以参考阅读 PCAWhitening。
深度学习中的 Internal Covariate Shift
深度神经网络模型的训练为什么会很困难?其中一个重要的原因是,深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。为了训好模型,我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。
Google 将这一现象总结为 Internal Covariate Shift,简称 ICS.
大家都知道在统计机器学习中的一个经典假设是“源空间(source domain)和目标空间(target domain)的数据分布(distribution)是一致的”。如果不一致,那么就出现了新的机器学习问题,如 transfer learning / domain adaptation 等。而 covariate shift 就是分布不一致假设之下的一个分支问题,它是指源空间和目标空间的条件概率是一致的,但是其边缘概率不同,即:对所有 \(x \in \mathcal{X}\) ,
$$P_{s}(Y | X=x)=P_{t}(Y | X=x)$$
但是
$$P_{s}(X) \neq P_{t}(X)$$
大家细想便会发现,的确,对于神经网络的各层输出,由于它们经过了层内操作作用,其分布显然与各层对应的输入信号分布不同,而且差异会随着网络深度增大而增大,可是它们所能“指示”的样本标记(label)仍然是不变的,这便符合了covariate shift的定义。由于是对层间信号的分析,也即是“internal”的来由。
ICS 会导致什么问题?
简而言之,每个神经元的输入数据不再是 “独立同分布”。
上层参数需要不断适应新的输入数据分布,降低学习速度。
下层输入的变化可能趋向于变大或者变小,导致上层落入饱和区,使得学习过早停止。
每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能的谨慎。
Normalization 的通用框架与基本思想
BN的基本思想其实相当直观:
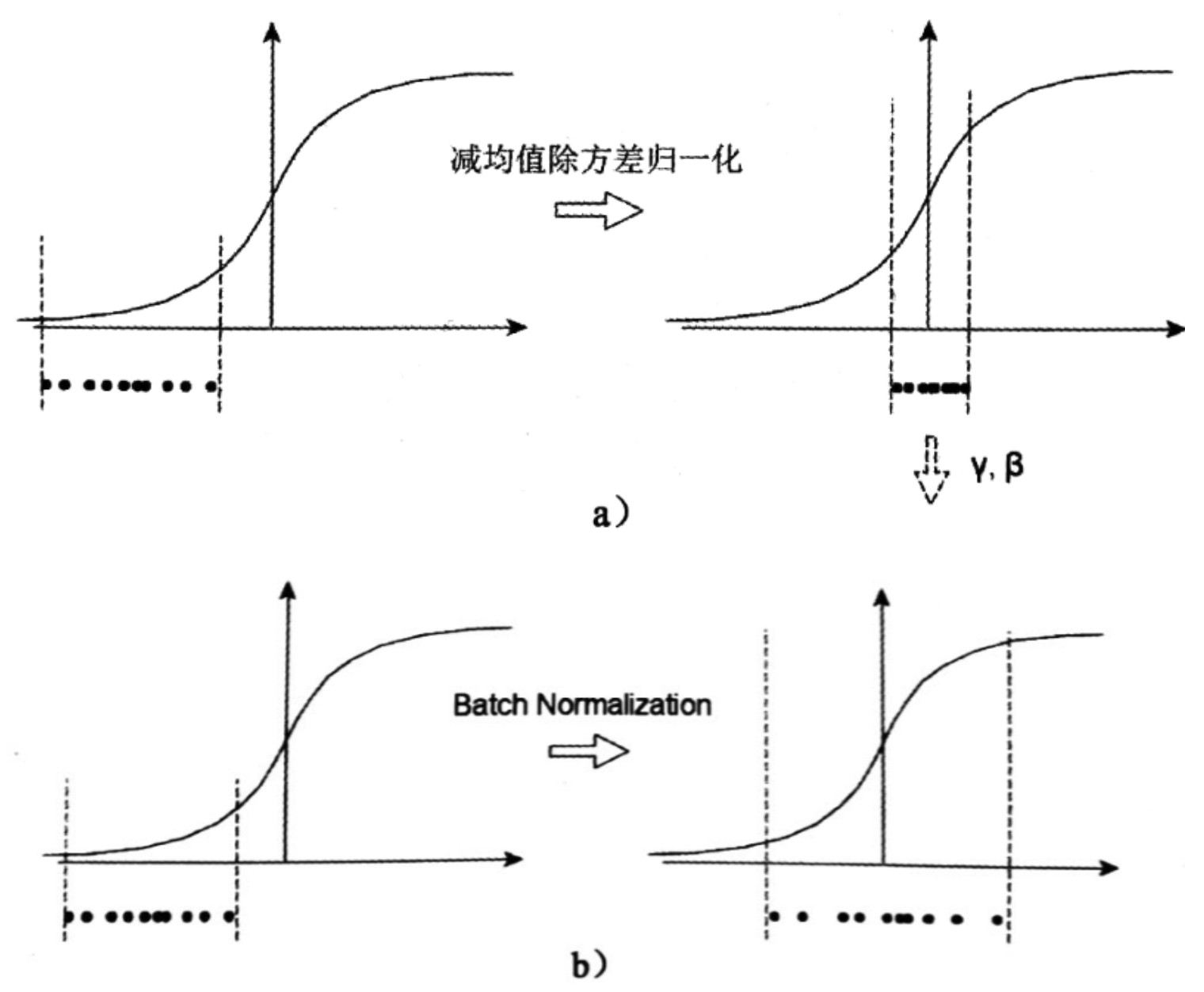
因为深层神经网络在做非线性变换前的激活输入值(就是那个x=WU+B,U是输入)随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(对于Sigmoid函数来说,意味着激活输入值WU+B是大的负值或正值),所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。
而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数较大的变化,意思是这样让梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
我们以神经网络中的一个普通神经元为例。神经元接收一组输入向量 \(\mathbf{x}=\left(x_{1}, x_{2}, \cdots, x_{d}\right)\) 通过某种运算后,输出一个标量值: \(y = f(\mathbf{x})\)
由于 ICS 问题的存在, \(\mathbf{x}\) 的分布可能相差很大。要解决独立同分布的问题,“理论正确”的方法就是对每一层的数据都进行白化操作。然而标准的白化操作代价高昂,特别是我们还希望白化操作是可微的,保证白化操作可以通过反向传播来更新梯度。
因此,以 BN 为代表的 Normalization 方法退而求其次,进行了简化的白化操作。基本思想是:在将 \(\mathbf{x}\) 送给神经元之前,先对其做平移和伸缩变换, 将 \(\mathbf{x}\) 的分布规范化成在固定区间范围的标准分布。
通用变换框架就如下所示:
$$
h=f\left(\mathbf{g} \cdot \frac{\mathbf{x}-\mu}{\sigma}+\mathbf{b}\right)
$$
我们来看看这个公式中的各个参数。
\(\mu\) 是平移参数(shift parameter), \(\sigma\) 是缩放参数(scale parameter)。通过这两个参数进行 shift 和 scale 变换: \(\hat{\mathbf{x}}=\frac{\mathbf{x}-\mu}{\sigma}\) 得到的数据符合均值为 0、方差为 1 的标准分布。
\(\mathbf{b}\) 是再平移参数(re-shift parameter),\(\mathbf{g}\) 是再缩放参数(re-scale parameter)。将 上一步得到的 \(\hat{\mathbf{x}}\) 进一步变换为:
$$
\mathbf{y}=\mathbf{g} \cdot \hat{\mathbf{x}}+\mathbf{b}
$$
最终得到的数据符合均值为 \(\mathbf{g}\) 、方差为 \(\mathbf{g}^{2}\) 的分布。
奇不奇怪?奇不奇怪?
说好的处理 ICS,第一步都已经得到了标准分布,第二步怎么又给变走了?
答案是 —— 为了保证模型的表达能力不因为规范化而下降。
我们可以看到,第一步的变换将输入数据限制到了一个全局统一的确定范围(均值为 0、方差为 1)。下层神经元可能很努力地在学习,但不论其如何变化,其输出的结果在交给上层神经元进行处理之前,将被粗暴地重新调整到这一固定范围。
难道我们底层神经元人民就在做无用功吗?
所以,为了尊重底层神经网络的学习结果,我们将规范化后的数据进行再平移和再缩放,使得每个神经元对应的输入范围是针对该神经元量身定制的一个确定范围(均值为 \(\mathbf{b}\) 、方差为 \(\mathbf{g}^{2}\) )。rescale 和 reshift 的参数都是可学习的,这就使得 Normalization 层可以学习如何去尊重底层的学习结果。
除了充分利用底层学习的能力,另一方面的重要意义在于保证获得非线性的表达能力。 Sigmoid 等激活函数在神经网络中有着重要作用,通过区分饱和区和非饱和区,使得神经网络的数据变换具有了非线性计算能力。而第一步的规范化会将几乎所有数据映射到激活函数的非饱和区(线性区),仅利用到了线性变化能力,从而降低了神经网络的表达能力。而进行再变换,则可以将数据从线性区变换到非线性区,恢复模型的表达能力。
经过这么的变回来再变过去,会不会跟没变一样?
不会。因为,再变换引入的两个新参数 g 和 b,可以表示旧参数作为输入的同一族函数,但是新参数有不同的学习动态。在旧参数中, \(\mathbf{X}\) 的均值取决于下层神经网络的复杂关联;但在新参数中, \(\mathbf{y}=\mathbf{g} \cdot \hat{\mathbf{x}}+\mathbf{b}\) 仅由 \(\mathbf{b}\) 来确定,去除了与下层计算的密切耦合。新参数很容易通过梯度下降来学习,简化了神经网络的训练。
这样的 Normalization 离标准的白化还有多远?
标准白化操作的目的是 “独立同分布”。独立就不说了,暂不考虑。变换为均值为\(\mathbf{b}\) 、方差为 \(\mathbf{g}^{2}\)的分布,也并不是严格的同分布,只是映射到了一个确定的区间范围而已。(所以,这个坑还有得研究呢!)
主流 Normalization 方法梳理
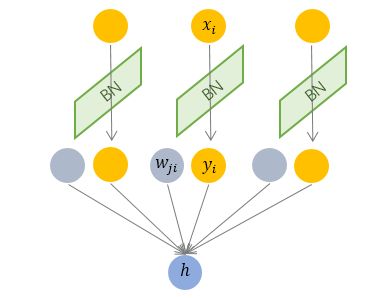
Batch Normalization 纵向规范化
$$
\mu_{i}=\frac{1}{M} \sum x_{i}, \quad \sigma_{i}=\sqrt{\frac{1}{M} \sum\left(x_{i}-\mu_{i}\right)^{2}+\epsilon}
$$
其中 \(\mathbf{M}\) 是 mini-batch 的大小。