机器学习汇总
基础知识
1. 参数法与非参数法
机器学习上的方法分:
参数方法
根据先验知识假定模型服从某种分布,然后利用训练集估计出模型参数,也就弄清楚了整个模型。
假设了一个在整个输入空间上有效的模型,将问题归结为在样本上估计少量参数,(如:线性模型估计w,高斯分布估计mu和sigma),参数学习方法假定了一个模型,当模型假定不成立或样本不是一个分组可能导致很大的误差。
例如感知器
非参数方法
不需要知道数据的概率分布,只需要假设:相似的输入具有相似的输出。基于记忆训练集,然后根据训练集预测。
非参数方法使用合适的距离度量相似性,对于输入样本,从训练集中找出它们的相似示例(输入样本的邻域),并由相似的实例插值得到正确的输入。
例如kNN
2. 维度灾难
Curse of Dimensionality
维度灾难是在数字图像处理中,对于已知样本数目,存在一个特征数目的最大值,当实际使用的特征数目超过这个最大值时,分类器的性能不是得到改善,而是退化。
这种现象正是在识别模式中被称为“维度灾难”的一种表现形式。此外,提取特征向量的维度过
高会增加计算的复杂度,给后续的分类问题造成负面影响。
非参数方法在特征数 p 很大时表现不好。
3. 分类器性能指标
3.1 ROC 曲线
receiver operating characteristics 接收者操作特征
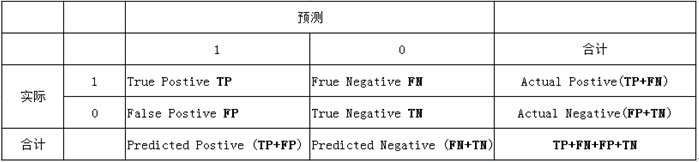
由上表可得出横,纵轴的计算公式:
真正类率 (True Postive Rate): \(TPR = \frac{TP}{TP+FN}\), 代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity
负正类率 (False Postive Rate) : \(FPR = \frac{FP}{FP+TN}\),代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity
真负类率 (True Negative Rate) : \(TNR = \frac{TN}{FP+TN}\),代表分类器预测的负类中实际负实例占所有负实例的比例, \(TNR=1-FPR\) 。Specificity
假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值如0.6,概率大于等于0.6的为正类,小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。
随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即TPR和FPR会同时增大。
阈值最大时,对应坐标点为 \((0,0)\) ,阈值最小时,对应坐标点 \((1,1)\) 。
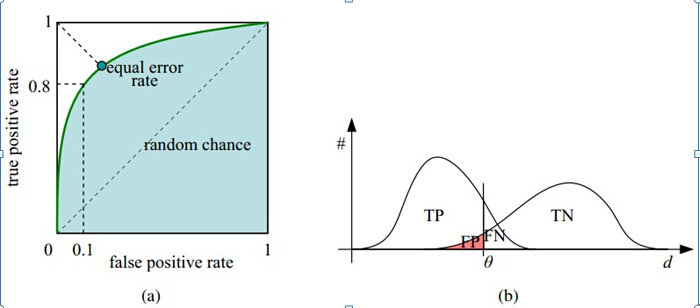
横轴:负正类率 (false postive rate FPR) 特异度,FPR越大,预测正类中实际负类越多。
纵轴:真正类率 (true postive rate TPR )灵敏度,TPR越大,预测正类中实际正类越多。
理想目标:
\(TPR=1,FPR=0\),即图中 \((0,1)\) 点,故ROC曲线越靠拢 \((0,1)\) 点,越偏离 45 度对角线越好,Sensitivity、Specificity 越大效果越好。
3.2 AUC
area under the curve
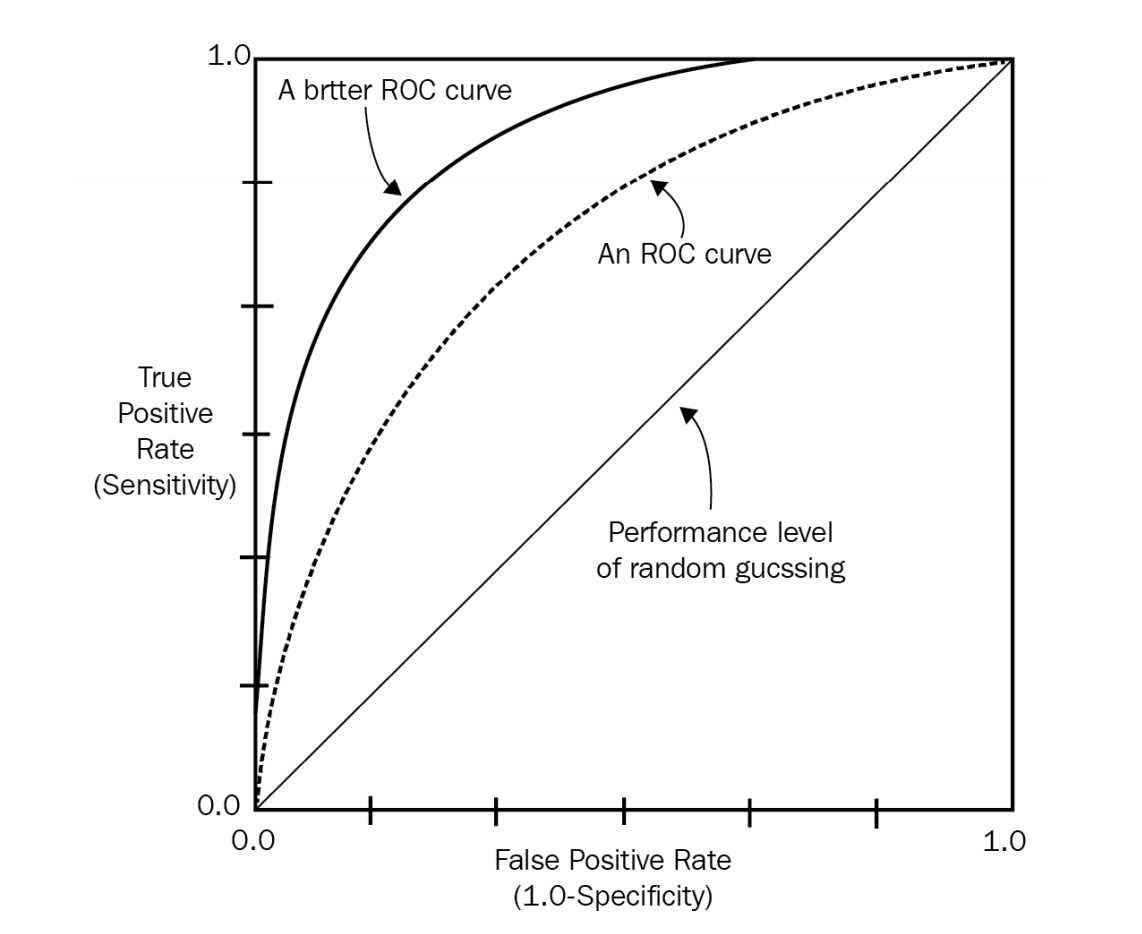
常常用AUC来评估二分类模型的性能
Roc 曲线下的面积,介于 0.1 和 1 之间。Auc 作为数值可以直观的评价分类器的好坏,值越大越好。
首先 AUC 值是一个概率值,当你随机挑选一个正样本以及负样本,当前的分类算法根据计算得到的Score 值将这个正样本排在负样本前面的概率就是 AUC 值,AUC 值越大,当前分类算法越有可能将正样本排在负样本前面,从而能够更好地分类。
AUC 可以看做随机从正负样本中选取一对正负样本,其中正样本的得分大于负样本的概率!
AUC 对正负样本比例不敏感
利用概率解释,还可以得到AUC另外一个性质,对正负样本比例不敏感。 在训练模型的时候,如果正负比例差异比较大,例如正负比例为1:1000,训练模型的时候通常要对负样本进行下采样。当一个模型训练完了之后,用负样本下采样后的测试集计算出来的AUC和未采样的测试集计算的AUC基本一致,或者说前者是后者的无偏估计!
方法
1. 梯度法
次梯度法(subgradient method)是传统梯度下降方法的拓展,用来处理不可微(non-differentiable )的凸函数。它的优势是比传统方法处理问题范围大,但劣势是算法收敛速度慢。而传统的梯度下降方法只能处理可导函数。

其实无论是梯度法还是次梯度法,本质上我们都在使用一阶泰勒展开式的原理去逼近在某点的原函数。正如泰勒展开式的思想所述,将目标函数在某点附近展开为泰勒(Taylor)多项式来逼近原函数。
1. 朴素贝叶斯

实例解析
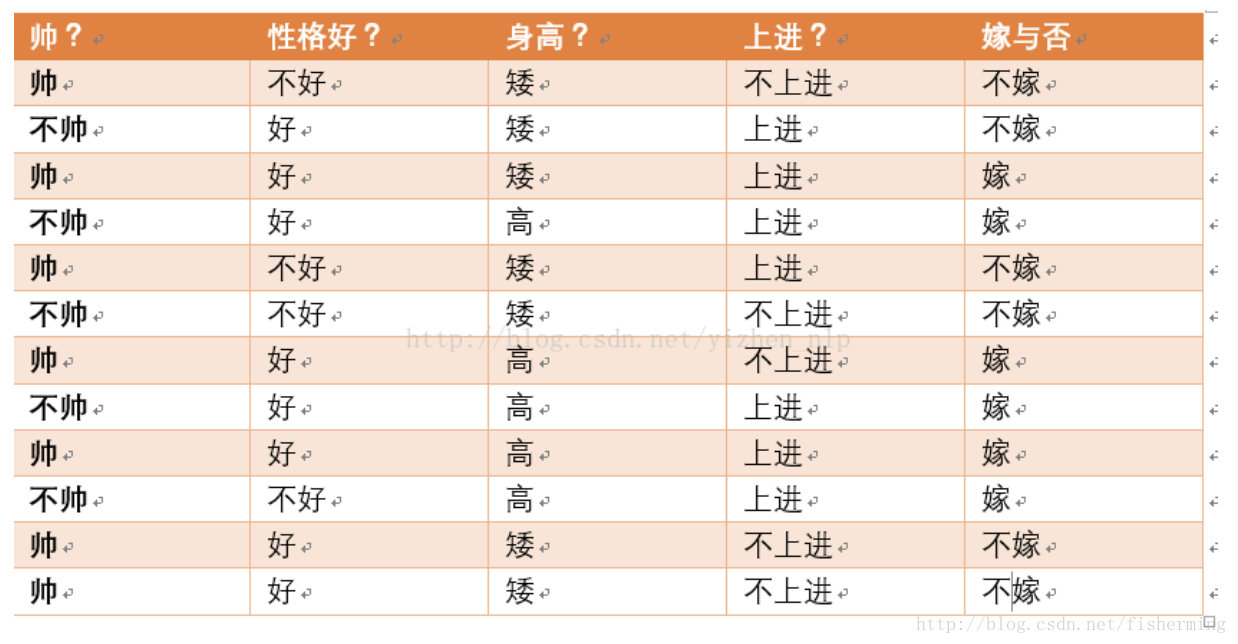
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是典型的二分类问题,按照朴素贝叶斯的求解,转换为
- \(P(嫁 | 不帅、性格不好、矮、不上进)\)
- \(P(不嫁 | 不帅、性格不好、矮、不上进)\)
的概率,最终选择嫁与不嫁的答案。
这里我们根据贝特斯公式:

$$P(不帅、性格不好、矮、不上进)=P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)$$
$$+P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)$$
$$P(不帅、性格不好、矮、不上进|嫁)=P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)$$
将上面的公式整理一下可得:

但是由贝叶斯公式可得:对于目标求解为不同的类别,贝叶斯公式的分母总是相同的。所以,只求解分子即可:
$$P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)=1/2 * 1/2 * 1/6 * 1/6 * 1/6=1/864$$
对于类别“不嫁”的贝叶斯分子为:
$$P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)=1/2 * 1/3 * 1/2 * 1* 2/3=1/18$$
经代入贝叶斯公式可得:
$$P(嫁|不帅、性格不好、矮、不上进)=(1/864) / (1/864+1/18)=1/49=2.04%$$
$$P(不嫁|不帅、性格不好、矮、不上进)=(1/18) / (1/864+1/18)=48/49=97.96%$$
则 \(P(不嫁|不帅、性格不好、矮、不上进) > P(嫁|不帅、性格不好、矮、不上进)\) ,则该女子选择不嫁!
优点:
- 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
- 分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
- 朴素贝叶斯假设属性之间相互独立,这种假设在实际过程中往往是不成立的。在属性之间相关性越大,分类误差也就越大。