基础

Numpy to Torth

python、PyTorch 图像读取与 numpy 转换

Torch 自称为神经网络界的 Numpy, 因为他能将 torch 产生的 tensor 放在 GPU 中加速运算 (前提是你有合适的 GPU), 就像 Numpy 会把 array 放在 CPU 中加速运算. 所以神经网络的话, 当然是用 Torch 的 tensor 形式数据最好咯. 就像 Tensorflow 当中的 tensor 一样.

当然, 我们对 Numpy 还是爱不释手的, 因为我们太习惯 numpy 的形式了. 不过 torch 看出来我们的喜爱, 他把 torch 做的和 numpy 能很好的兼容. 比如这样就能自由地转换 numpy array 和 torch tensor 了:

import torch
import numpy as np

np_data = np.arange(6).reshape((2, 3))
torch_data = torch.from_numpy(np_data)
tensor2array = torch_data.numpy()
print(
    '\nnumpy array:', np_data,          # [[0 1 2], [3 4 5]]
    '\ntorch tensor:', torch_data,      #  0  1  2 \n 3  4  5    [torch.LongTensor of size 2x3]
    '\ntensor to array:', tensor2array, # [[0 1 2], [3 4 5]]
)

数学运算

其实 torch 中 tensor 的运算和 numpy array 的如出一辙, 我们就以对比的形式来看. 如果想了解 torch 中其它更多有用的运算符, API 就是你要去的地方

# abs 绝对值计算
data = [-1, -2, 1, 2]
tensor = torch.FloatTensor(data)  # 转换成32位浮点 tensor
print(
    '\nabs',
    '\nnumpy: ', np.abs(data),          # [1 2 1 2]
    '\ntorch: ', torch.abs(tensor)      # [1 2 1 2]
)

# sin   三角函数 sin
print(
    '\nsin',
    '\nnumpy: ', np.sin(data),      # [-0.84147098 -0.90929743  0.84147098  0.90929743]
    '\ntorch: ', torch.sin(tensor)  # [-0.8415 -0.9093  0.8415  0.9093]
)

# mean  均值
print(
    '\nmean',
    '\nnumpy: ', np.mean(data),         # 0.0
    '\ntorch: ', torch.mean(tensor)     # 0.0
)

除了简单的计算, 矩阵运算才是神经网络中最重要的部分. 所以我们展示下矩阵的乘法. 注意一下包含了一个 numpy 中可行, 但是 torch 中不可行的方式

# matrix multiplication 矩阵点乘
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data)  # 转换成32位浮点 tensor
# correct method
print(
    '\nmatrix multiplication (matmul)',
    '\nnumpy: ', np.matmul(data, data),     # [[7, 10], [15, 22]]
    '\ntorch: ', torch.mm(tensor, tensor)   # [[7, 10], [15, 22]]
)

# !!!!  下面是错误的方法 !!!!
data = np.array(data)
print(
    '\nmatrix multiplication (dot)',
    '\nnumpy: ', data.dot(data),        # [[7, 10], [15, 22]] 在numpy 中可行
    '\ntorch: ', tensor.dot(tensor)     # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0
)

新版本中(>=0.3.0), 关于 tensor.dot() 有了新的改变, 它只能针对于一维的数组. 所以上面的有所改变

tensor.dot(tensor)     # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0

# 变为
torch.dot(tensor.dot(tensor)

Variable

在 Torch 中的 Variable 就是一个存放会变化的值的地理位置. 里面的值会不停的变化. 就像一个裝鸡蛋的篮子, 鸡蛋数会不停变动. 那谁是里面的鸡蛋呢, 自然就是 Torch 的 Tensor 咯. 如果用一个 Variable 进行计算, 那返回的也是一个同类型的 Variable.

import torch
from torch.autograd import Variable # torch 中 Variable 模块

# 先生鸡蛋
tensor = torch.FloatTensor([[1,2],[3,4]])
# 把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor, requires_grad=True)

print(tensor)
"""
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable)
"""
Variable containing:
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

获取 Variable 里面的数据

直接 print(variable) 只会输出 Variable 形式的数据, 在很多时候是用不了的(比如想要用 plt 画图), 所以我们要转换一下, 将它变成 tensor 形式.

print(variable)     #  Variable 形式
"""
Variable containing:
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable.data)    # tensor 形式
"""
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable.data.numpy())    # numpy 形式
"""
[[ 1.  2.]
 [ 3.  4.]]
"""

激励函数

导入模块

1
2
3

import torch
import torch.nn.functional as F     # 激励函数都在这
from torch.autograd import Variable

做一些假数据来观看图像

1
2
3

x = torch.linspace(-5, 5, 200)  # x data (tensor), shape=(100, 1)
x = Variable(x)
x_np = x.data.numpy()  # 换成 numpy array, 出图时用

不同的激励函数

# 几种常用的 激励函数
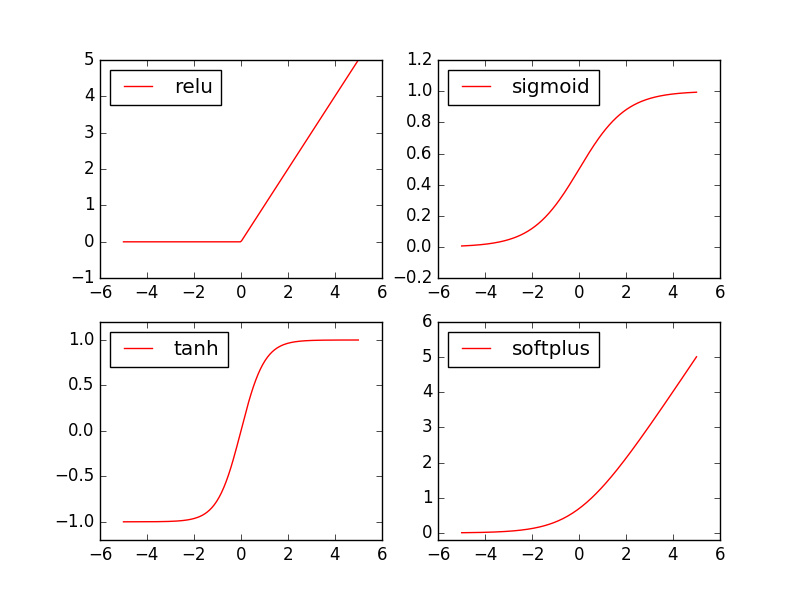
y_relu = F.relu(x).data.numpy()
y_sigmoid = F.sigmoid(x).data.numpy()
y_tanh = F.tanh(x).data.numpy()
y_softplus = F.softplus(x).data.numpy()
# y_softmax = F.softmax(x)  softmax 比较特殊, 不能直接显示, 不过他是关于概率的, 用于分类

观察图像

import matplotlib.pyplot as plt  

plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')

plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')

plt.subplot(223)
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')

plt.subplot(224)
plt.plot(x_np, y_softplus, c='red', label='softplus')
plt.ylim((-0.2, 6))
plt.legend(loc='best')

plt.show()

数据处理

DataLoader

Torch 中提供了一种帮你整理你的数据结构的好东西, 叫做 DataLoader, 我们能用它来包装自己的数据, 进行批训练. 而且批训练可以有很多种途径

DataLoader

DataLoader 是 torch 给你用来包装你的数据的工具. 所以你要讲自己的 (numpy array 或其他) 数据形式装换成 Tensor, 然后再放进这个包装器中. 使用 DataLoader 有什么好处呢? 就是他们帮你有效地迭代数据, 举例:

import torch
import torch.utils.data as Data
torch.manual_seed(1)    # reproducible

BATCH_SIZE = 5      # 批训练的数据个数

x = torch.linspace(1, 10, 10)       # x data (torch tensor)
y = torch.linspace(10, 1, 10)       # y data (torch tensor)

# 先转换成 torch 能识别的 Dataset
torch_dataset = Data.TensorDataset(x, y)

# 把 dataset 放入 DataLoader
loader = Data.DataLoader(
    dataset=torch_dataset,      # torch TensorDataset format
    batch_size=BATCH_SIZE,      # mini batch size
    shuffle=True,               # 要不要打乱数据 (打乱比较好)
    num_workers=2,              # 多线程来读数据
)

for epoch in range(3):   # 训练所有!整套!数据 3 次
    for step, (batch_x, batch_y) in enumerate(loader):  # 每一步 loader 释放一小批数据用来学习
        # 假设这里就是你训练的地方...

        # 打出来一些数据
        print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
              batch_x.numpy(), '| batch y: ', batch_y.numpy())

"""
Epoch:  0 | Step:  0 | batch x:  [ 6.  7.  2.  3.  1.] | batch y:  [  5.   4.   9.   8.  10.]
Epoch:  0 | Step:  1 | batch x:  [  9.  10.   4.   8.   5.] | batch y:  [ 2.  1.  7.  3.  6.]
Epoch:  1 | Step:  0 | batch x:  [  3.   4.   2.   9.  10.] | batch y:  [ 8.  7.  9.  2.  1.]
Epoch:  1 | Step:  1 | batch x:  [ 1.  7.  8.  5.  6.] | batch y:  [ 10.   4.   3.   6.   5.]
Epoch:  2 | Step:  0 | batch x:  [ 3.  9.  2.  6.  7.] | batch y:  [ 8.  2.  9.  5.  4.]
Epoch:  2 | Step:  1 | batch x:  [ 10.   4.   8.   1.   5.] | batch y:  [  1.   7.   3.  10.   6.]
"""

可以看出, 每步都导出了5个数据进行学习. 然后每个 epoch 的导出数据都是先打乱了以后再导出.

ImageFolder

1
2
3

from torchvision.datasets import ImageFolder

ImageFolder(root,transform=None,target_transform=None,loader=default_loader)

假设所有的文件按文件夹保存好，每个文件夹下面存贮同一类别的图片，文件夹的名字为分类的名字。

root: 在指定的 root 路径下面寻找图片
transform: 对 PIL Image 进行转换操作,transform 输入是 loader 读取图片返回的对象
target_transform: 对 label 进行变换
loader: 指定加载图片的函数，默认操作是读取 PIL image 对象

实例

1
2
3

from torchvision.datasets import ImageFolder

dataset=ImageFolder('data/dogcat_2/')

输出对应文件夹的 label

1
2
3

print(dataset.class_to_idx)    

# {'cat': 0, 'dog': 1}

所有图片的路径和对应的 label

1
2
3

print(dataset.imgs)  

# [(‘data/dogcat_2/cat/cat.12484.jpg’, 0), (‘data/dogcat_2/cat/cat.12485.jpg’, 0), ... (‘data/dogcat_2/dog/dog.12498.jpg’, 1), (‘data/dogcat_2/dog/dog.12499.jpg’, 1)]

输出图片信息

print(dataset[0][1]) #第二维度为1 ，表示label
print(dataset[0][0]) #第二维度为0，表示图片数据

# 输出: 
# 0 
# < PIL.Image.Image image mode=RGB size=497x500 at 0x7F25F3D31E10>

输出图片大小

# 输出第 0 张图片的大小
print(dataset[0][0].size())

# torch.Size([3, 224, 224])

加上 transforms

from torchvision.datasets import ImageFolder
import torch
from torchvision import transforms

#加上transforms
normalize=transforms.Normalize(mean=[.5,.5,.5],std=[.5,.5,.5])
transform=transforms.Compose([
    transforms.RandomReSizedCrop(224),
    transforms.RandomHorizontalFlip(),
    transforms.ToTensor(), #将图片转换为Tensor,归一化至[0,1]
    normalize
])

dataset=ImageFolder('data/dogcat_2/',transform=transform)
print(dataset[0][0].size())    # n输出第 0 张图片的大小

# torch.Size([3, 224, 224])

最后使用时仍需 DataLoader 包装

1	dataloader = torch.utils.data.DataLoader(dataset, batch_size=opt.batchSize, shuffle=True, num_workers=opt.workers)

图像处理

transforms的二十二个方法

定义自己的数据集

不使用 ImageFolder 来处理定义自己的数据集

#数据处理
import os
import torch
from torch.utils import data
from PIL import Image
import numpy as np
from torchvision import transforms

transform=transforms.Compose([
    transforms.Resize(224), #缩放图片，保持长宽比不变，最短边的长为224像素,
    transforms.CenterCrop(224), #从中间切出 224*224的图片
    transforms.ToTensor(), #将图片转换为Tensor,归一化至[0,1]
    transforms.Normalize(mean=[.5,.5,.5],std=[.5,.5,.5]) #标准化至[-1,1]
])

#定义自己的数据集合
class DogCat(data.Dataset):

    def __init__(self,root):
        #所有图片的绝对路径
        imgs=os.listdir(root)

        self.imgs=[os.path.join(root,k) for k in imgs]
        self.transforms=transform

    def __getitem__(self, index):
        img_path=self.imgs[index]
        #dog-> 1 cat ->0
        label=1 if 'dog' in img_path.split('/')[-1] else 0
        pil_img=Image.open(img_path)
        if self.transforms:
            data=self.transforms(pil_img)
        else:
            pil_img=np.asarray(pil_img)
            data=torch.from_numpy(pil_img)
        return data,label

    def __len__(self):
        return len(self.imgs)

dataSet=DogCat('./data/dogcat')

print(dataSet[0])

单张图片

# load and process an image, e.g.
transform = transforms.Compose([
    transforms.Resize(256),
    transforms.CenterCrop(224),
    transforms.ToTensor(),
    transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])

# do the object recognition
im = transform(Image.open('test_image.jpg'))
pred = object_recognition(im.unsqueeze(0))

网络搭建

回归

建立数据集

我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它.

import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())                 # noisy y data (tensor), shape=(100, 1)

# 用 Variable 来修饰这些数据 tensor
x, y = torch.autograd.Variable(x), Variable(y)

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

建立神经网络

建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性 (__init__()), 然后再一层层搭建(forward(x))层于层的关系链接

import torch
import torch.nn.functional as F     # 激励函数都在这

class Net(torch.nn.Module):  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()     # 继承 __init__ 功能
        # 定义每层用什么样的形式
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.predict = torch.nn.Linear(n_hidden, n_output)   # 输出层线性输出

    def forward(self, x):   # 这同时也是 Module 中的 forward 功能
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.predict(x)             # 输出值
        return x

net = Net(n_feature=1, n_hidden=10, n_output=1)

print(net)  # net 的结构
"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""

训练网络

# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)  # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss()      # 预测值和真实值的误差计算公式 (均方差)

for t in range(100):
    prediction = net(x)     # 喂给 net 训练数据 x, 输出预测值

    loss = loss_func(prediction, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

可视化训练过程

import matplotlib.pyplot as plt

plt.ion()   # 画图
plt.show()

for t in range(100):

    ...  # 同上
    loss.backward()
    optimizer.step()

    # 接着上面来
    if t % 5 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'Loss=%.4f' % loss.data[0], fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

分类

建立数据集

import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt

# 假数据
n_data = torch.ones(100, 2)         # 数据的基本形态
x0 = torch.normal(2*n_data, 1)      # 类型0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100)               # 类型0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1)     # 类型1 x data (tensor), shape=(100, 1)
y1 = torch.ones(100)                # 类型1 y data (tensor), shape=(100, 1)

# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor)  # FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor)    # LongTensor = 64-bit integer

# torch 只能在 Variable 上训练, 所以把它们变成 Variable
x, y = Variable(x), Variable(y)

# plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
# plt.show()

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show(

建立神经网络

import torch
import torch.nn.functional as F     # 激励函数都在这

class Net(torch.nn.Module):     # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()     # 继承 __init__ 功能
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.out = torch.nn.Linear(n_hidden, n_output)       # 输出层线性输出

    def forward(self, x):
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.out(x)                 # 输出值, 但是这个不是预测值, 预测值还需要再另外计算
        return x

net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output

print(net)  # net 的结构
"""
Net (
  (hidden): Linear (2 -> 10)
  (out): Linear (10 -> 2)
)
"""

训练网络

# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.02)  # 传入 net 的所有参数, 学习率
# 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,)
# 但是预测值是2D tensor (batch, n_classes)
loss_func = torch.nn.CrossEntropyLoss()

for t in range(100):
    out = net(x)     # 喂给 net 训练数据 x, 输出分析值

    loss = loss_func(out, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

可视化训练过程

import matplotlib.pyplot as plt

plt.ion()   # 画图
plt.show()

for t in range(100):

    ...
    loss.backward()
    optimizer.step()

    # 接着上面来
    if t % 2 == 0:
        plt.cla()
        # 过了一道 softmax 的激励函数后的最大概率才是预测值
        prediction = torch.max(F.softmax(out), 1)[1]
        pred_y = prediction.data.numpy().squeeze()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
        accuracy = sum(pred_y == target_y)/200  # 预测中有多少和真实值一样
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

plt.ioff()  # 停止画图
plt.show()

快速搭建

我们先看看之前写神经网络时用到的步骤. 我们用 net1 代表这种方式搭建的神经网络.

class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.predict = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = F.relu(self.hidden(x))
        x = self.predict(x)
        return x

net1 = Net(1, 10, 1)   # 这是我们用这种方式搭建的 net1

我们用 class 继承了一个 torch 中的神经网络结构, 然后对其进行了修改, 不过还有更快的一招, 用一句话就概括了上面所有的内容!

net2 = torch.nn.Sequential(
    torch.nn.Linear(1, 10),
    torch.nn.ReLU(),
    torch.nn.Linear(10, 1)
)

我们再对比一下两者的结构:

print(net1)
"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""
print(net2)
"""
Sequential (
  (0): Linear (1 -> 10)
  (1): ReLU ()
  (2): Linear (10 -> 1)
)
"""

我们会发现 net2 多显示了一些内容, 这是为什么呢? 原来他把激励函数也一同纳入进去了, 但是 net1 中, 激励函数实际上是在 forward() 功能中才被调用的. 这也就说明了, 相比 net2, net1 的好处就是, 你可以根据你的个人需要更加个性化你自己的前向传播过程, 比如(RNN). 不过如果不需要七七八八的过程, 相信 net2 这种形式更适合.

保存与提取

我们快速地建造数据, 搭建网络:

torch.manual_seed(1)    # reproducible

# 假数据
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())  # noisy y data (tensor), shape=(100, 1)
x, y = Variable(x, requires_grad=False), Variable(y, requires_grad=False)


def save():
    # 建网络
    net1 = torch.nn.Sequential(
        torch.nn.Linear(1, 10),
        torch.nn.ReLU(),
        torch.nn.Linear(10, 1)
    )
    optimizer = torch.optim.SGD(net1.parameters(), lr=0.5)
    loss_func = torch.nn.MSELoss()

    # 训练
    for t in range(100):
        prediction = net1(x)
        loss = loss_func(prediction, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

接下来我们有两种途径来保存

1 2	torch.save(net1, 'net.pkl') # 保存整个网络 torch.save(net1.state_dict(), 'net_params.pkl') # 只保存网络中的参数 (速度快, 占内存少)

提取

提取整个神经网络, 网络大的时候可能会比较慢

这个方法要 import 原来的 pytorch 模型类，或者直接将该类复制回来

class CNN(nn.Module):
	...

net2 = torch.load('net.pkl') # net.pkl 中保存的类要和上边的 CNN 类相同
prediction = net2(x)

只提取网络参数

这个方法会提取所有的参数，然后再放到你的新建网络中

def restore_params():
    # 新建 net3
    net3 = torch.nn.Sequential(
        torch.nn.Linear(1, 10),
        torch.nn.ReLU(),
        torch.nn.Linear(10, 1)
    )

    # 将保存的参数复制到 net3
    net3.load_state_dict(torch.load('net_params.pkl'))
    prediction = net3(x)

显示结果

# 保存 net1 (1. 整个网络, 2. 只有参数)
save()

# 提取整个网络
restore_net()

# 提取网络参数, 复制到新网络
restore_params()

这样我们能看到三个网络一模一样

优化器 Optimizer

伪数据

import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt

torch.manual_seed(1)    # reproducible

LR = 0.01
BATCH_SIZE = 32
EPOCH = 12

# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))

# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()

# 使用上节内容提到的 data loader
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)

每个优化器优化一个神经网络

为了对比每一种优化器, 我们给他们各自创建一个神经网络, 但这个神经网络都来自同一个 Net 形式

# 默认的 network 形式
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)   # hidden layer
        self.predict = torch.nn.Linear(20, 1)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

# 为每个优化器创建一个 net
net_SGD         = Net()
net_Momentum    = Net()
net_RMSprop     = Net()
net_Adam        = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]

优化器 Optimizer

接下来在创建不同的优化器, 用来训练不同的网络. 并创建一个 loss_func 用来计算误差. 我们用几种常见的优化器, SGD, Momentum, RMSprop, Adam.

# different optimizers
opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]

loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []]   # 记录 training 时不同神经网络的 loss

训练/出图

for epoch in range(EPOCH):
    print('Epoch: ', epoch)
    for step, (b_x, b_y) in enumerate(loader):

        # 对每个优化器, 优化属于他的神经网络
        for net, opt, l_his in zip(nets, optimizers, losses_his):
            output = net(b_x)              # get output for every net
            loss = loss_func(output, b_y)  # compute loss for every net
            opt.zero_grad()                # clear gradients for next train
            loss.backward()                # backpropagation, compute gradients
            opt.step()                     # apply gradients
            l_his.append(loss.data.numpy())     # loss recoder

SGD 是最普通的优化器, 也可以说没有加速效果, 而 Momentum 是 SGD 的改良版, 它加入了动量原则. 后面的 RMSprop 又是 Momentum 的升级版. 而 Adam 又是 RMSprop 的升级版. 不过从这个结果中我们看到, Adam 的效果似乎比 RMSprop 要差一点. 所以说并不是越先进的优化器, 结果越佳. 我们在自己的试验中可以尝试不同的优化器, 找到那个最适合你数据/网络的优化器

卷积神经网络

MNIST手写数据

import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision      # 数据库模块
import matplotlib.pyplot as plt

torch.manual_seed(1)    # reproducible

# Hyper Parameters
EPOCH = 1           # 训练整批数据多少次, 为了节约时间, 我们只训练一次
BATCH_SIZE = 50
LR = 0.001          # 学习率
DOWNLOAD_MNIST = True  # 如果你已经下载好了mnist数据就写上 Fasle


# Mnist 手写数字
train_data = torchvision.datasets.MNIST(
    root='./mnist/',    # 保存或者提取位置
    train=True,  # this is training data
    transform=torchvision.transforms.ToTensor(),    # 转换 PIL.Image or numpy.ndarray 成
                                                    # torch.FloatTensor (C x H x W), 训练的时候 normalize 成 [0.0, 1.0] 区间
    download=DOWNLOAD_MNIST,          # 没下载就下载, 下载了就不用再下了
)

同样, 我们除了训练数据, 还给一些测试数据, 测试看看它有没有训练好

test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)

# 批训练 50samples, 1 channel, 28x28 (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

# 为了节约时间, 我们测试时只测试前2000个
test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000]/255.   # shape from (2000, 28, 28) to (2000, 1, 28, 28), value in range(0,1)
test_y = test_data.test_labels[:2000]

CNN模型

和以前一样, 我们用一个 class 来建立 CNN 模型. 这个 CNN 整体流程是卷积(Conv2d) -> 激励函数(ReLU) -> 池化, 向下采样 (MaxPooling) -> 再来一遍 -> 展平多维的卷积成的特征图 -> 接入全连接层 (Linear) -> 输出

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(  # input shape (1, 28, 28)
            nn.Conv2d(
                in_channels=1,      # input height
                out_channels=16,    # n_filters
                kernel_size=5,      # filter size
                stride=1,           # filter movement/step
                padding=2,      # 如果想要 con2d 出来的图片长宽没有变化, padding=(kernel_size-1)/2 当 stride=1
            ),      # output shape (16, 28, 28)
            nn.ReLU(),    # activation
            nn.MaxPool2d(kernel_size=2),    # 在 2x2 空间里向下采样, output shape (16, 14, 14)
        )
        self.conv2 = nn.Sequential(  # input shape (16, 14, 14)
            nn.Conv2d(16, 32, 5, 1, 2),  # output shape (32, 14, 14)
            nn.ReLU(),  # activation
            nn.MaxPool2d(2),  # output shape (32, 7, 7)
        )
        self.out = nn.Linear(32 * 7 * 7, 10)   # fully connected layer, output 10 classes

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = x.view(x.size(0), -1)   # 展平多维的卷积图成 (batch_size, 32 * 7 * 7)
        output = self.out(x)
        return output

cnn = CNN()
print(cnn)  # net architecture
"""
CNN (
  (conv1): Sequential (
    (0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (1): ReLU ()
    (2): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
  )
  (conv2): Sequential (
    (0): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (1): ReLU ()
    (2): MaxPool2d (size=(2, 2), stride=(2, 2), dilation=(1, 1))
  )
  (out): Linear (1568 -> 10)
)
"""

训练

下面我们开始训练, 将 x y 都用 Variable 包起来, 然后放入 cnn 中计算 output, 最后再计算误差. 下面代码省略了计算精确度 accuracy 的部分

optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)   # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss()   # the target label is not one-hotted

# training and testing
for epoch in range(EPOCH):
    for step, (b_x, b_y) in enumerate(train_loader):   # 分配 batch data, normalize x when iterate train_loader
        output = cnn(b_x)               # cnn output
        loss = loss_func(output, b_y)   # cross entropy loss
        optimizer.zero_grad()           # clear gradients for this training step
        loss.backward()                 # backpropagation, compute gradients
        optimizer.step()                # apply gradients

"""
...
Epoch:  0 | train loss: 0.0306 | test accuracy: 0.97
Epoch:  0 | train loss: 0.0147 | test accuracy: 0.98
Epoch:  0 | train loss: 0.0427 | test accuracy: 0.98
Epoch:  0 | train loss: 0.0078 | test accuracy: 0.98
"""

最后我们再来取10个数据, 看看预测的值到底对不对:

test_output = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')

"""
[7 2 1 0 4 1 4 9 5 9] prediction number
[7 2 1 0 4 1 4 9 5 9] real number
"""

网络优化方法

1. Dropout

做点数据

自己做一些伪数据, 用来模拟真实情况. 数据少, 才能凸显过拟合问题, 所以我们就做10个数据点

import torch
import matplotlib.pyplot as plt

torch.manual_seed(1)    # reproducible

N_SAMPLES = 20
N_HIDDEN = 300

# training data
x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))

# test data
test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))

# show data
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.show()

搭建神经网络

我们在这里搭建两个神经网络, 一个没有 dropout, 一个有 dropout. 没有 dropout 的容易出现过拟合, 那我们就命名为 net_overfitting, 另一个就是 net_dropped. torch.nn.Dropout(0.5) 这里的 0.5 指的是随机有 50% 的神经元会被关闭/丢弃.

net_overfitting = torch.nn.Sequential(
    torch.nn.Linear(1, N_HIDDEN),
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, N_HIDDEN),
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, 1),
)

net_dropped = torch.nn.Sequential(
    torch.nn.Linear(1, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, 1),
)

训练

训练的时候, 这两个神经网络分开训练. 训练的环境都一样

optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(), lr=0.01)
optimizer_drop = torch.optim.Adam(net_dropped.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()

for t in range(500):
    pred_ofit = net_overfitting(x)
    pred_drop = net_dropped(x)

    loss_ofit = loss_func(pred_ofit, y)
    loss_drop = loss_func(pred_drop, y)

    optimizer_ofit.zero_grad()
    optimizer_drop.zero_grad()
    loss_ofit.backward()
    loss_drop.backward()
    optimizer_ofit.step()
    optimizer_drop.step()

对比测试结果

在这个 for 循环里, 我们加上画测试图的部分. 注意在测试时, 要将网络改成 eval() 形式, 特别是 net_dropped, net_overfitting 改不改其实无所谓. 画好图再改回 train() 模式

...

optimizer_ofit.step()
optimizer_drop.step()

# 接着上面来
if t % 10 == 0:     # 每 10 步画一次图
    # 将神经网络转换成测试形式, 画好图之后改回 训练形式
    net_overfitting.eval()
    net_dropped.eval()  # 因为 drop 网络在 train 的时候和 test 的时候参数不一样.

    ...
    test_pred_ofit = net_overfitting(test_x)
    test_pred_drop = net_dropped(test_x)
    ...

    # 将两个网络改回 训练形式
    net_overfitting.train()
    net_dropped.train()

2. Batch Normalization

批标准化通俗来说就是对每一层神经网络进行标准化 (normalize) 处理, 我们知道对输入数据进行标准化能让机器学习有效率地学习. 如果把每一层后看成这种接受输入数据的模式, 那我们何不 “批标准化” 所有的层呢?

做点数据

自己做一些伪数据, 用来模拟真实情况. 而且 Batch Normalization (之后都简称BN) 还能有效的控制坏的参数初始化 (initialization), 比如说 ReLU 这种激励函数最怕所有的值都落在附属区间, 那我们就将所有的参数都水平移动一个 -0.2 (bias_initialization = -0.2), 来看看 BN 的实力.

import torch
from torch import nn
from torch.nn import init
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as np

# 超参数
N_SAMPLES = 2000
BATCH_SIZE = 64
EPOCH = 12
LR = 0.03
N_HIDDEN = 8
ACTIVATION = F.tanh     # 你可以换 relu 试试
B_INIT = -0.2   # 模拟不好的 参数初始化

# training data
x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise

# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise

train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x = torch.from_numpy(test_x).float()
test_y = torch.from_numpy(test_y).float()

train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)

# show data
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')
plt.show()

搭建神经网络

这里就教你如何构建带有 BN 的神经网络的. BN 其实可以看做是一个 layer (BN layer). 我们就像平时加层一样加 BN layer 就好了. 注意, 我还对输入数据进行了一个 BN 处理, 因为如果你把输入数据看出是从前面一层来的输出数据, 我们同样也能对她进行 BN.

class Net(nn.Module):
    def __init__(self, batch_normalization=False):
        super(Net, self).__init__()
        self.do_bn = batch_normalization
        self.fcs = []   # 太多层了, 我们用 for loop 建立
        self.bns = []
        self.bn_input = nn.BatchNorm1d(1, momentum=0.5)   # 给 input 的 BN

        for i in range(N_HIDDEN):               # 建层
            input_size = 1 if i == 0 else 10
            fc = nn.Linear(input_size, 10)
            setattr(self, 'fc%i' % i, fc)       # 注意! pytorch 一定要你将层信息变成 class 的属性! 我在这里花了2天时间发现了这个 bug
            self._set_init(fc)                  # 参数初始化
            self.fcs.append(fc)
            if self.do_bn:
                bn = nn.BatchNorm1d(10, momentum=0.5)
                setattr(self, 'bn%i' % i, bn)   # 注意! pytorch 一定要你将层信息变成 class 的属性! 我在这里花了2天时间发现了这个 bug
                self.bns.append(bn)

        self.predict = nn.Linear(10, 1)         # output layer
        self._set_init(self.predict)            # 参数初始化

    def _set_init(self, layer):     # 参数初始化
        init.normal_(layer.weight, mean=0., std=.1)
        init.constant_(layer.bias, B_INIT)

    def forward(self, x):
        pre_activation = [x]
        if self.do_bn: x = self.bn_input(x)    # 判断是否要加 BN
        layer_input = [x]
        for i in range(N_HIDDEN):
            x = self.fcs[i](x)
            pre_activation.append(x)    # 为之后出图
            if self.do_bn: x = self.bns[i](x)  # 判断是否要加 BN
            x = ACTIVATION(x)
            layer_input.append(x)       # 为之后出图
        out = self.predict(x)
        return out, layer_input, pre_activation

# 建立两个 net, 一个有 BN, 一个没有
nets = [Net(batch_normalization=False), Net(batch_normalization=True)]

训练

opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]

loss_func = torch.nn.MSELoss()

losses = [[], []]  # 每个网络一个 list 来记录误差
for epoch in range(EPOCH):
    print('Epoch: ', epoch)
    for step, (b_x, b_y) in enumerate(train_loader):
        for net, opt in zip(nets, opts):     # 训练两个网络
            pred, _, _ = net(b_x)
            loss = loss_func(pred, b_y)
            opt.zero_grad()
            loss.backward()
            opt.step()    # 这也会训练 BN 里面的参数

画图

f, axs = plt.subplots(4, N_HIDDEN+1, figsize=(10, 5))

def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
    ...

for epoch in range(EPOCH):
    layer_inputs, pre_acts = [], []
    for net, l in zip(nets, losses):
        # 一定要把 net 的设置成 eval 模式, eval下的 BN 参数会被固定
        net.eval()
        pred, layer_input, pre_act = net(test_x)
        l.append(loss_func(pred, test_y).data[0])
        layer_inputs.append(layer_input)
        pre_acts.append(pre_act)
        # 收集好信息后将 net 设置成 train 模式, 继续训练
        net.train()
    plot_histogram(*layer_inputs, *pre_acts)     # plot histogram

    # 后面接着之前 for loop 中的代码来
    for step, (b_x, b_y) in enumerate(train_loader):
    ...

GPU 训练

我们定义一个辅助函数，以便在有 GPU 时选择 GPU 为目标设备，否则就默认选择 CPU。

def get_default_device():
    """Pick GPU if available, else CPU"""
    if torch.cuda.is_available():
        return torch.device('cuda')
    else:
        return torch.device('cpu')

1
2
3

device = get_default_device()

print(device)   # device(type='cuda')

CUDA memory error

lower resolution, though hurt performance
use gradient accumulation to get a larger batch size
duly use empty_cache or use other methods to manage memory finely
use pytorch checkpoint to run partial model at once

多 GPU 训练

import torch.nn as nn

model=nn.DataParallel(model,device_ids=[0,1,2]) # multi-GPU
model=nn.DataParallel(model) # multi-GPU

函数

维度调整

import numpy as np
import torch

a = np.arange(24).reshape(2,3,4)
b = a[:,-1,:]
print(b.shape)

# (2, 4)

x = torch.from_numpy(a)
y = x[:,-1,:].unsqueeze(1)
print(y.size())     # torch.Size([2, 1, 4])
z = y.expand(2,4,4)
print(z.size())     # torch.Size([2, 4, 4])

expand

扩展某个size为1的维度。如(2,2,1)扩展为(2,2,3)

import torch
x=torch.randn(2,2,1)
print(x)
y=x.expand(2,2,3)
print(y)

输出：

tensor([[ 0.2000,  0.3000,  0.2000],
        [ 1.3000,  1.3000,  1.3000],
        [ 2.3000,  2.3000,  2.3000],
        [ 3.2000,  3.2000,  3.1000]])
tensor([[ 1.1000,  2.2000,  1.3000],
        [ 2.1000,  2.2000,  2.3000],
        [ 2.1000,  2.2000,  2.3000],
        [ 1.1000,  1.2000,  0.3000]])
tensor([[ 0.2000],
        [ 1.3000],
        [ 2.1000],
        [ 3.2000]])

squeeze

将维度为1的压缩掉。如size为（3,1,1,2），压缩之后为（3,2）

import torch
a=torch.randn(2,1,1,3)
print(a)
print(a.squeeze())

输出：

tensor([[[[-0.2320,  0.9513,  1.1613]]],
 
 
        [[[ 0.0901,  0.9613, -0.9344]]]])
tensor([[-0.2320,  0.9513,  1.1613],
        [ 0.0901,  0.9613, -0.9344]])

unsqueeze(n)

在第 n 个位置增加一维，如 (2,3) 在 unsqueeze(1) 后为 (2,1,3)
可以用来增加 batch 的位置

max

返回最大值，或指定维度的最大值以及 index

argmax

返回最大值的 index

pytorch之expand，gather，squeeze，sum，contiguous，softmax，max，argmax

错误汇总

Pytorch 错误汇总

1	Expected stride to be a single integer value or a list of 1 values to match the convolution dimensions, but got stride=[1, 1]

model 输入 tensor 错误，形状应为 batch, c, w, h

1	AttributeError: Can't get attribute 'Net' on <module '__main__'>

在导入模型的时候没有把类的定义添加或者 import 到加载模型的这个 py 文件中

1	Expected more than 1 value per channel when training, got input size torch.Size([1, 512, 1, 1])

可能是输入批次只有一个数据点，而由于BatchNorm操作需要多于一个数据计算平均值，因此造成该错误。

解决方法：

改变（增大） batchsize
在获取数据集时，将DataLoader中drop_last设置为True。
把不够一个批次的数据丢弃。

浩瀚宇宙·AaronChen

PyTorch 总结

基础