1 Algorithm 算法

  • An algorithm is a step-by-step procedure for performing some task in a finite amount of time.

1.1 Principle of algorithm analysis

How do we define a“good” algorithm?

  • Running time is a natural measure of “goodness,” since time is a precious resource—computer solutions should run as fast as possible
  • Space usage is another major issue to consider when we design an algorithm, since we only have limited storage spaces

Measuring the running time:

1
2
3
4
5
6
7
8
9
10
11
from time import time

startTime = time()

for i in range(20000000):
    if i % 100000 == 0:
        print(1)

endTime = time()

print('time: %f seconds' % (endTime - startTime))

1) Counting primitive operations

To analyse the running time of an algorithm without performing experiments, we perform an analysis directly on a high-level description of the algorithm

primitive operations:

  • Assigning an identifier to an object
  • Determining the object associated with an identifier
  • Performing an arithmetic operation (for example, adding two numbers)
  • Comparing two numbers
  • Accessing a single element of a Python list by index
  • Calling a function (excluding operations executed within the function)
  • Returning from a function.

2) Measuring Operations as a Function of Input Size

To capture the order of growth of an algorithm’s running time, we will associate, with each algorithm, a function f(n) that characterizes the number of primitive operations that are performed as a function of the input size n.

3) Focusing on the Worst-Case Input

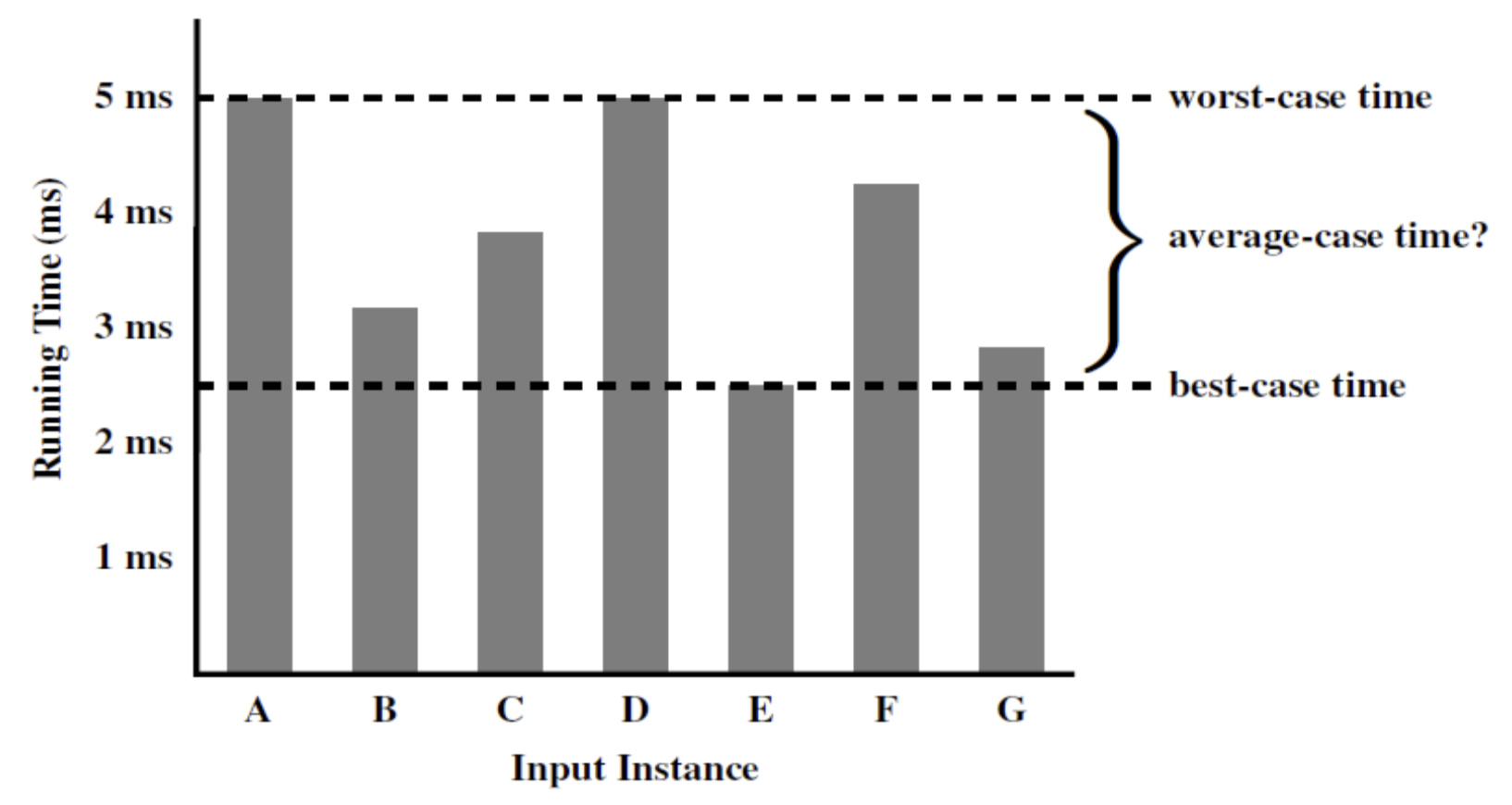
1.2 algorithm analysis

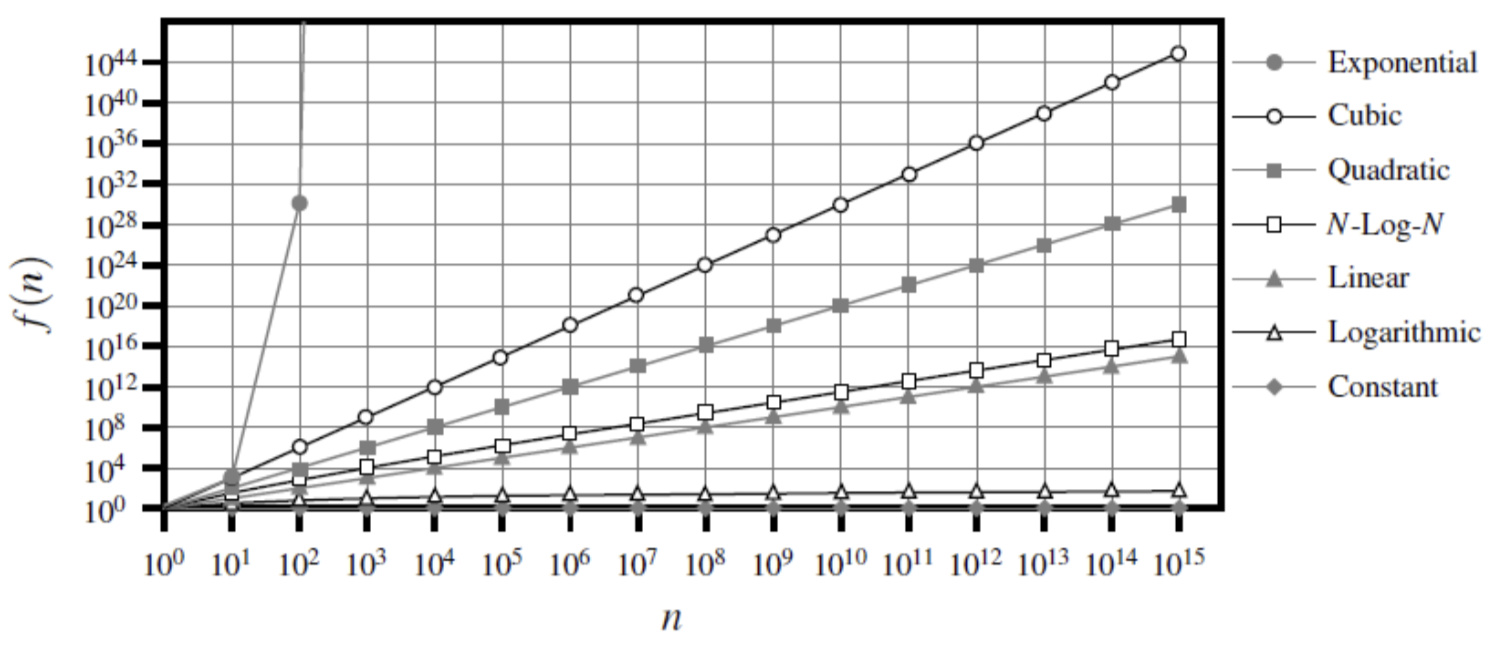
1) The 7 functions used in algorithm analysis

We may use the following 7 functions to measure the time complexity of an algorithm:

  • constant
  • logarithm
  • linear
  • N-log-N
  • quadratic
  • cubic and other polynomials
  • exponential

2) Asymptotic Analysis 渐进分析

  • In algorithm analysis, we focus on the growth rate of the running time as a function of the input size n, taking a “big-picture” approach
  • Vocabulary for the analysis and design of algorithms
  • “Sweet spot” for high-level reasoning about algorithms
  • Coarse enough to supress unnecessary details, e.g. architecture/language/compiler…
  • Sharp enough to make meaningful comparisons between algorithms

3) The big Oh notation

  • Let f(n) and g(n) be functions mapping positive integers to positive real numbers.
  • We say that f(n) is O(g(n)) if there is a real constant c > 0 and an integer constant n0 ≥ 1 such that
    f(n) ≤ cg(n), for n ≥ n0
  • This definition is often referred to as the “big-Oh” notation
  • Example: The function 8n+5 is O(n), g(n) = n c = 9, n0 = 10

4) Some Properties of the Big-Oh Notation

The big-Oh notation allows us to ignore constant factors and lower-order terms and focus on the main components of a function that affect its growth.

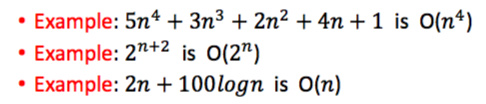
In general, we should use the big-Oh notation to characterize a function as closely as possible

1.3 Comparative analysis

Q:
An algorithm A, which has a running time of ( O(n), and an algorithm B, which has a running time of O(𝑛 ). Which algorithm is better?

A:
Algorithm A is asymptotically (渐近) better than algorithm B, Constant of A may very large ,so it is not always better than b.

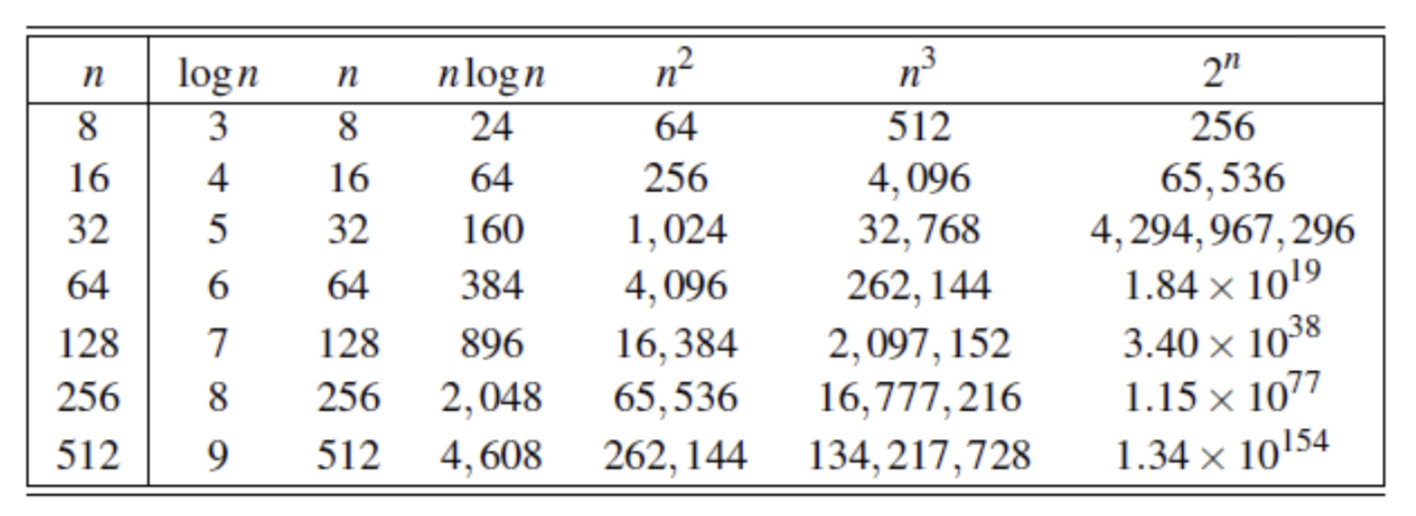
1) The line of tractability

  • To differentiate efficient and inefficient algorithms, the general line is between polynomial time algorithms and exponential time algorithms
  • The distinction between polynomial-time and exponential- time algorithms is considered a robust measure of tractability

1.4 Recursion 递归

1) definition

  • First, a recursive definition contains one or more base cases, which are defined non-recursively in terms of fixed quantities
  • Second, it also contains one or more recursive cases, which are defined by appealing to the definition of the function being defined

2) How Python implements recursion

  • In Python, each time a function (recursive or otherwise) is called, a structure known as an activation record or frame is created to store information about the progress of that invocation of the function
  • This activation record stores the function call’s parameters and local variables (哪个函数被call了，函数的参数parametersxg，call这个函数的位置location)
  • When the execution of a function leads to a nested function call, the execution of the former call is suspended（悬挂，暂停） and its activation record stores the place in the source code at which the flow of control should continue upon return of the nested call

3) The recursive trace

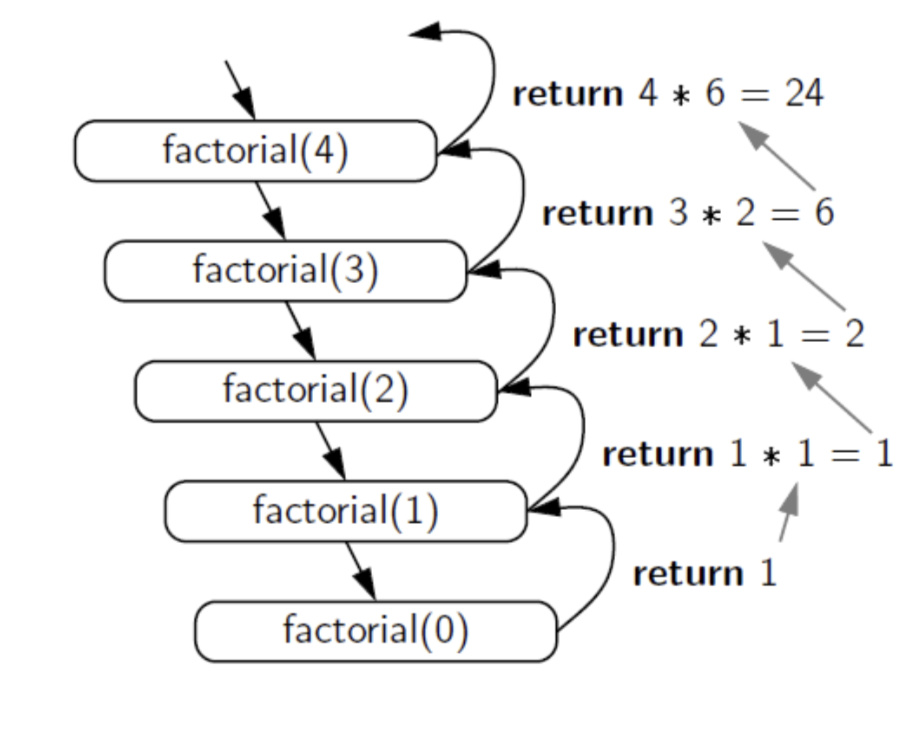
4) 递归算法的通用结构：

1
2
3
4
def f():
	make()
	if check():
		f()

1.5 Binary search 二分法

A classic and very useful recursive algorithm.

When the sequence is unsorted, the standard approach to search for a target value is to use a loop to examine every element, until either finding the target or exhausting the data set; This is known as the sequential search algorithm

Code:

Time complexity:

The binary search algorithm runs in O(logn) time for a sorted sequence with n elements.

N *（1/2）^x = 1 —-> x = logn

1.6 Bubble sort 冒泡排序

Its general procedure is:

  1. Iterate over a list of numbers, compare every element i with the following element i+1, and swap them if i is larger
  2. Iterate over the list again and repeat the procedure in step 1, but ignore the last element in the list
  3. Continuously iterate over the list, but each time ignore one more element at the tail of the list, until there is only one element left

Code

1.7 Quick sort 快速排序

1) 分治思想

快速排序采用的思想是分治思想

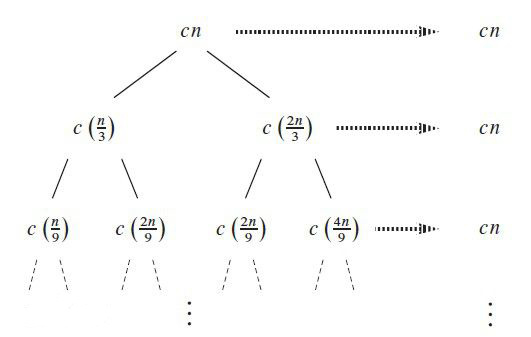
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可以得到原问题的解。下面这张图会说明分治算法是如何进行的：将cn分成了两个cn/2，转而分成了cn/4，cn/8……我们通过这样一层一层的求解规模小的子问题，将其合并之后就能求出原问题的解。

2) 快速排序

• The main procedure of quick sort algorithm is:

  1. Pick an element, called a pivot, from the array
  2. Partitioning: reorder the array so that:

  • all elements with values less than the pivot come before the pivot,

  • while all elements with values greater than the pivot come after it

  • (equal values can go either way).

    After this partitioning, the pivot is in its final position. This is called the partition operation

  1. Recursively 递归 apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values

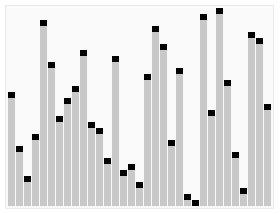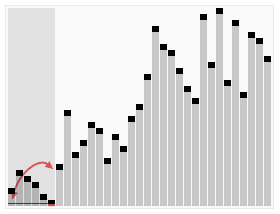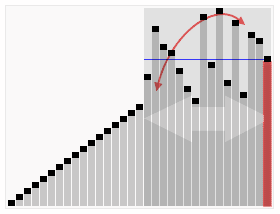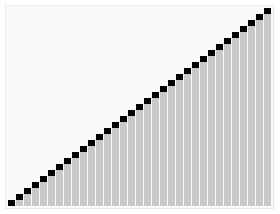
时间复杂度最理想 O(nlogn) 最差情况（原数列已经有序） O(n^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def QuickSort(myList, start, end):

    # 判断low是否小于high,如果为false,直接返回
    if start < end:
        i,j = start,end
        # 设置基准数
        # i负责找比base小的数，j负责找比base大的数
        base = myList[i]

        while i < j:
            # 如果列表后边的数,比基准数大或相等,则前移一位直到有比基准数小的数出现
            while (i < j) and (myList[j] >= base):
                j = j - 1

            # 如找到,则把第j个元素赋值给第个元素i,此时表中i,j个元素相等
            myList[i] = myList[j]

            # 同样的方式比较前半区
            while (i < j) and (myList[i] <= base):
                i = i + 1
            myList[j] = myList[i]
        # 做完第一轮比较之后,列表被分成了两个半区,并且i=j,需要将这个数设置回base
        myList[i] = base

        # 递归前半区
        QuickSort(myList, start, i - 1)
        # 递归后半区
        QuickSort(myList, j + 1, end)
    return myList
    
myList = [49,38,65,97,76,13,27,49]
QuickSort(myList, 0, len(myList)-1)

交换类似于交叉交换：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
[6, 1, 2, 7, 9, 3, 4, 5, 10, 8]
 ·                    ·
[5, 1, 2, 7, 9, 3, 4, 5, 10, 8]
          ·           ·
[5, 1, 2, 7, 9, 3, 4, 7, 10, 8]
          ·        ·
[5, 1, 2, 4, 9, 3, 4, 7, 10, 8]
             ·     ·
[5, 1, 2, 4, 9, 3, 9, 7, 10, 8]
             ·  ·
[5, 1, 2, 4, 3, 3, 9, 7, 10, 8]
                ·
[5, 1, 2, 4, 3, 3, 9, 7, 10, 8]
                ·
[5, 1, 2, 4, 3, 6, 9, 7, 10, 8]

2 Data structure 数据结构

  • A data structure is a systematic way of organizing and accessing data

2.1 stack 堆栈

  • A stack is a collection of objects that are inserted and removed according to the last-in, first-out (LIFO) principle.
  • A user may insert objects into a stack at any time, but may only access or remove the most recently inserted object that remains (at the so-called “top” of the stack).

1) example

Web Browser

  • Internet Web browsers store the addresses of recently visited sites in a stack. Each time a user visits a new site, that site’s address is “pushed” onto the stack of addresses. The browser then allows the user to “pop” back to previously visited sites using the “back” button.

Text editor

  • Text editors usually provide an “undo” mechanism that cancels recent editing operations and reverts to former states of a document. This undo operation can be accomplished by keeping text changes in a stack.

2) The stack class

Generally, a stack may contain the following methods:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class ListStack:

    def __init__(self):
        self.__data = list()

    def __len__(self):
        return len(self.__data)

    def is_empty(self):
        return len(self.__data) == 0

    def push(self, e):
        self.__data.append(e)

    def top(self):
        if self.is_empty():
            print('The stack is empty.')
        else:
            return self.__data[self.__len__()-1]

    def pop(self):
        if self.is_empty():
            print('The stack is empty.')
        else:
            return self.__data.pop()

    def __str__(self):
        return str(self.__data)

    def __repr__(self):
        return str(self)

3) Practice

  1. Reverse a list using stack

  1. Brackets match checking

  1. Matching Tags in HTML Language

2.2 Queue 队列

  • Queue is another fundamental data structure
  • A queue is a collection of objects that are inserted and
    removed according to the first-in, first-out (FIFO) principle
  • Elements can be inserted at any time, but only the element that has been in the queue the longest can be next removed

1) the queue class

The queue class may contain the following methods:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
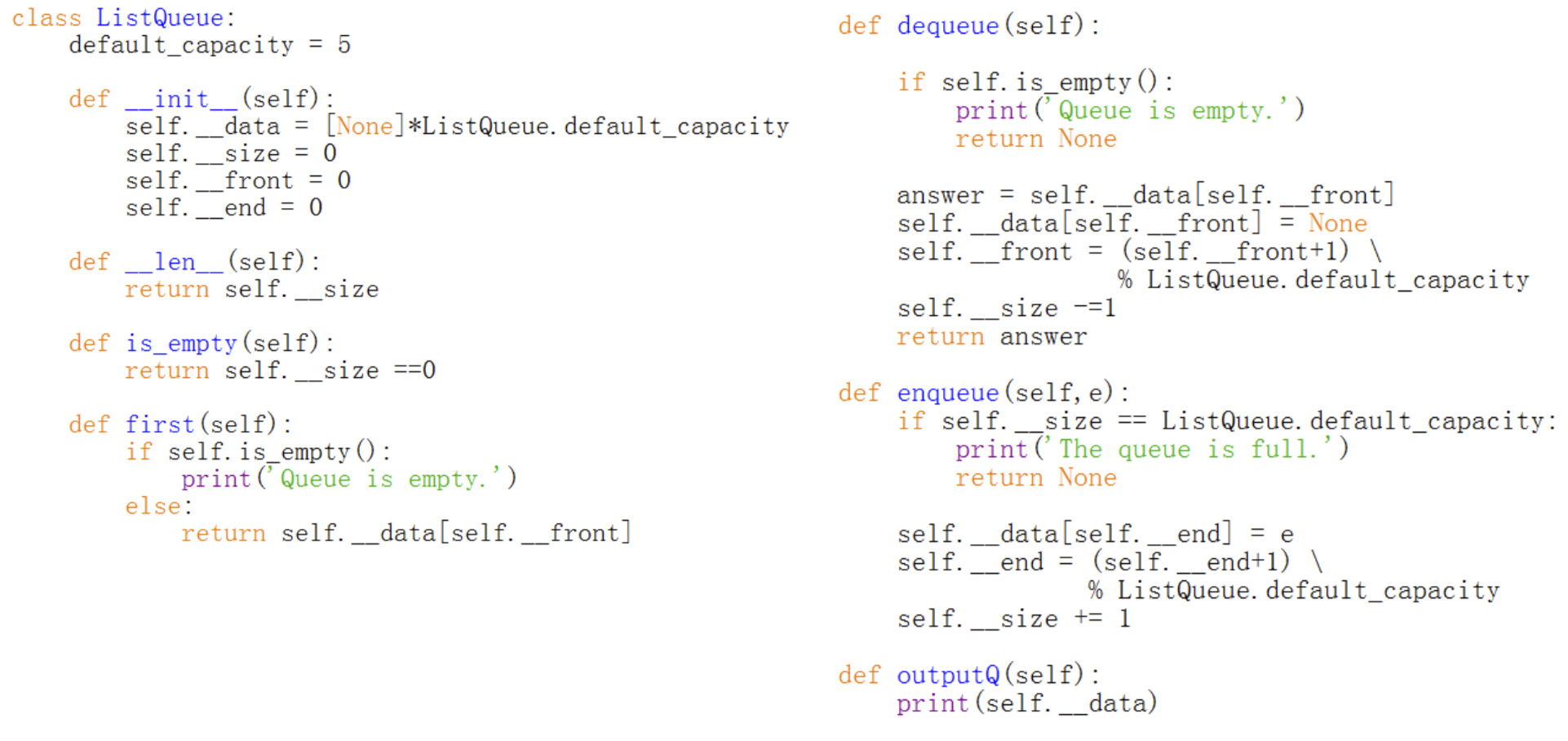
45
class ListQueue:
    default_capacity = 10

    def __init__(self):
        self.__data = [None] * ListQueue.default_capacity
        self.__size = 0
        self.__front = 0
        self.__end = 0


    def __len__(self):
        return self.__size

    def is_empty(self):
        return self.__size == 0

    def first(self):
        if self.is_empty():
            print('Queue is empty.')
        else:
            return self.__data[self.__front]

    def dequeue(self):
        if self.is_empty():
            print('Queue is empty.')
            return None
        else:
            answer = self.__data[self.__front]
            self.__data[self.__front] = None
            self.__front = (self.__front + 1) % ListQueue.default_capacity
            self.__size -= 1
            return answer

    def enqueue(self,e):
        if self.__size == ListQueue.default_capacity:
            print('The queue is full.')
        else:
            self.__data[self.__end] = e
            self.__end = (self.__end + 1) % ListQueue.default_capacity
            self.__size += 1

    def __str__(self):
        return str(self.__data)
    def __repr__(self):
        return str(self)

2) Practice: Simulating a web service

An online video website handles service requests in the following way:

  1. It maintains a service queue which stores all the unprocessed service requests.
  2. When a new service request arrives, it will be saved at the end of the service queue.
  3. The server of the website will process each service request on a “first-come-first-serve” basis.

2.3 Linked list 链表

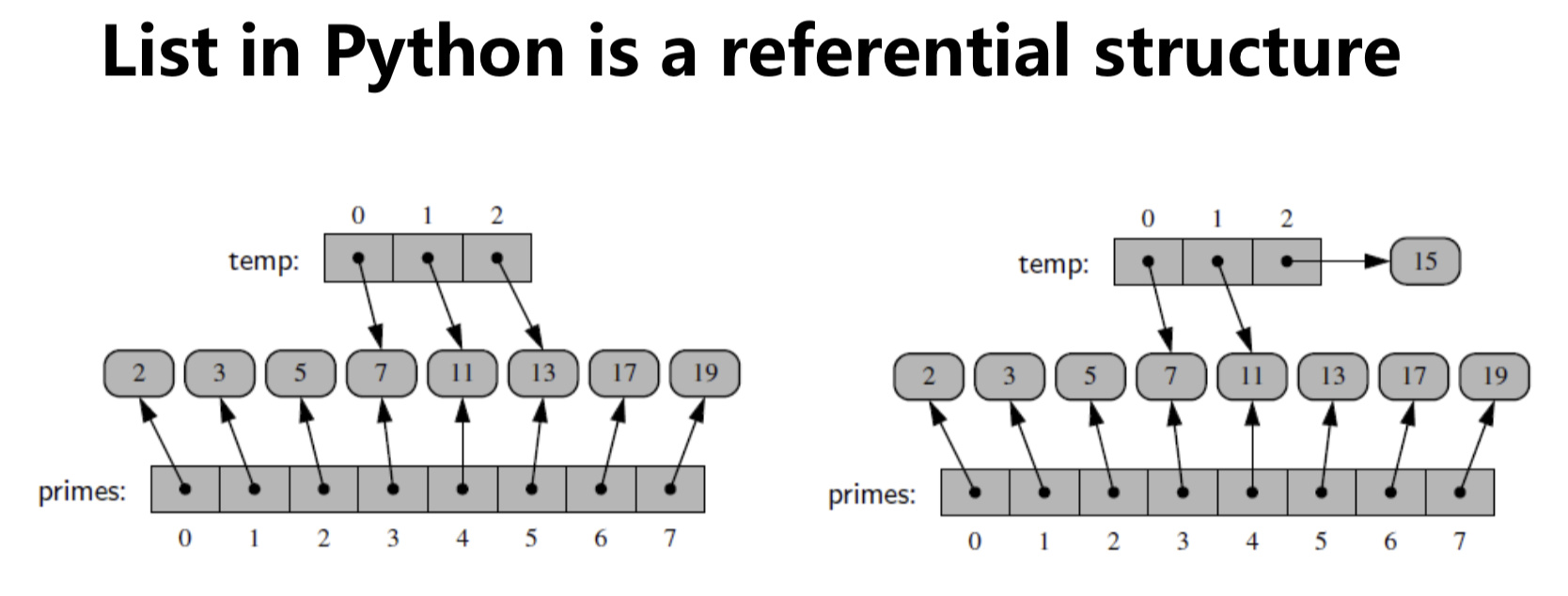
1) list in python

  • Python’s list class is highly optimized, and often a great choice for storage
  • However, many programming languages do not support this kind of optimized list data type

同一个值可以被不同的list分享

同一个list的相同值也可以在同一个id地址

2) Compact array

  • A collection of numbers are usually stored as a compact array in languages such as C/C++ and Java
  • A compact array is storing the bits that represent the primary data (not reference)
  • The overall memory usage will be much lower for a compact structure because there is no overhead devoted to the explicit storage of the sequence of memory references (in addition to the primary data)

3) Linked List

链表是一个基础的数据结构，可以使用链表去实现其他各种数据结构

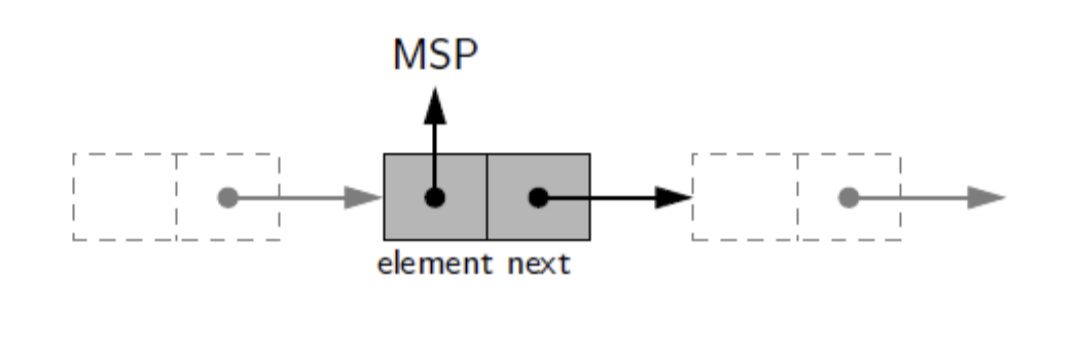
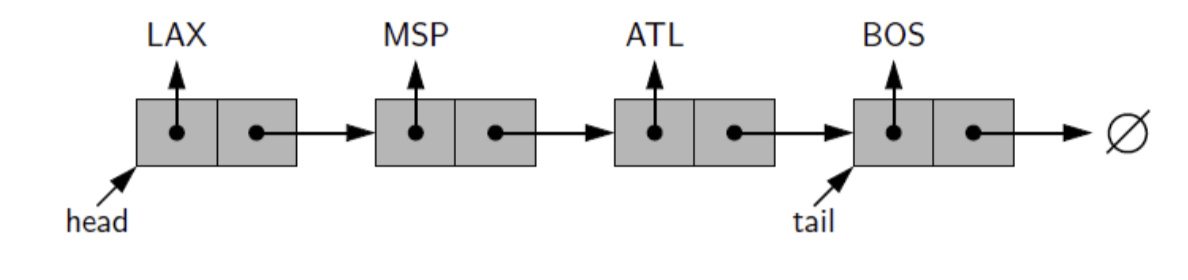
  • A singly linked list, in its simplest form, is a collection of nodes that collectively form a linear sequence
  • Each node stores a reference to an object that is an element of the sequence, as well as a reference to the next node of the list

内存地址不一定是连续的

  • The first and last nodes of a linked list are known as the head and tail of the list, respectively
  • By starting at the head, and moving from one node to another by following each node’s next reference, we can reach the tail of the list
  • We can identify the tail as the node having None as its next reference. This process is commonly known as traversing the linked list.
  • Because the next reference of a node can be viewed as a link or pointer to another node, the process of traversing a list is also known as link hopping or pointer hopping

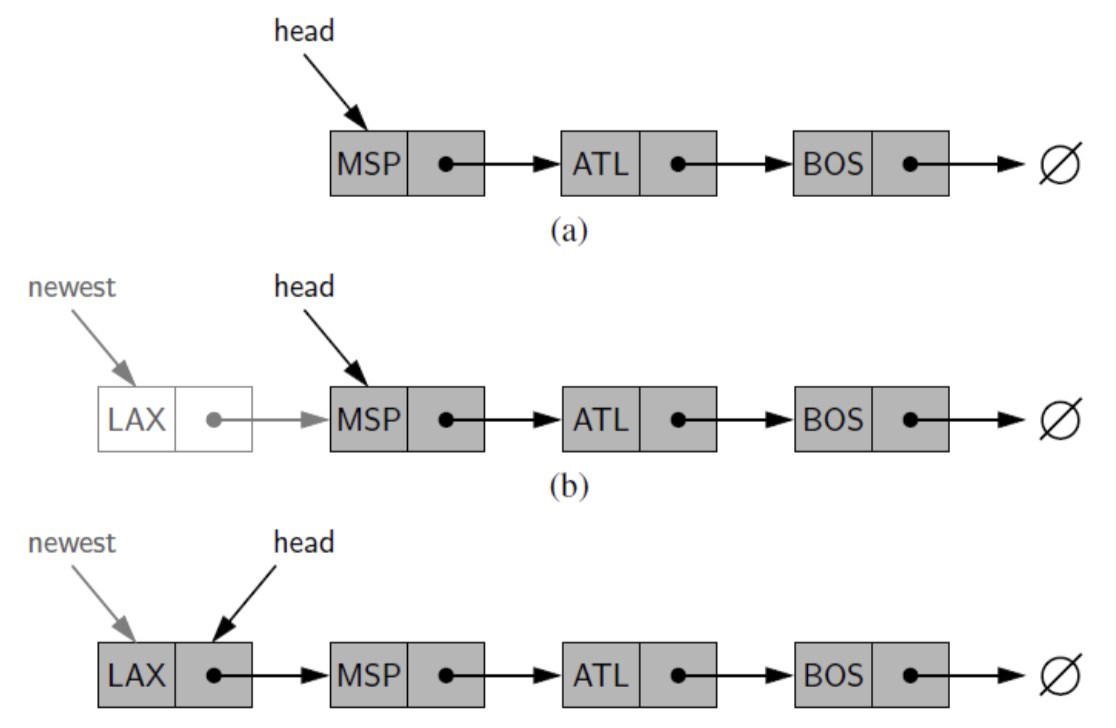
4) Inserting an Element at the Head

5) Inserting an Element at the Tail

不论首尾首先先新建一个Node

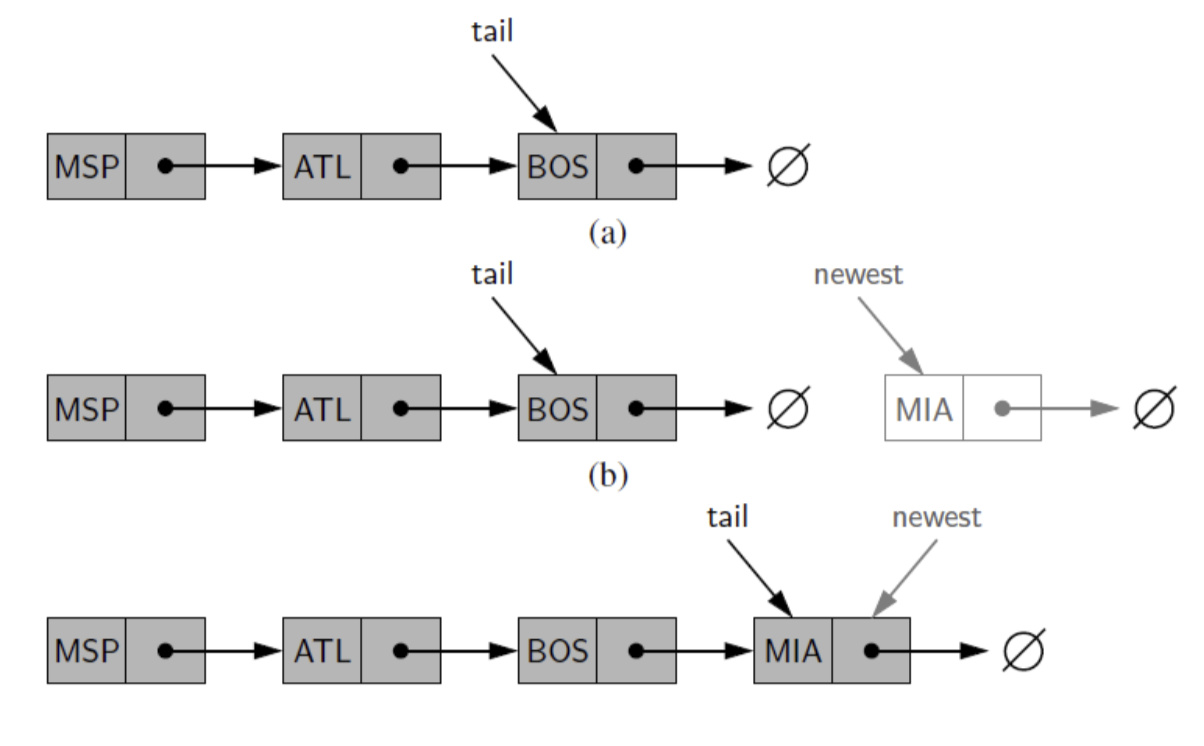
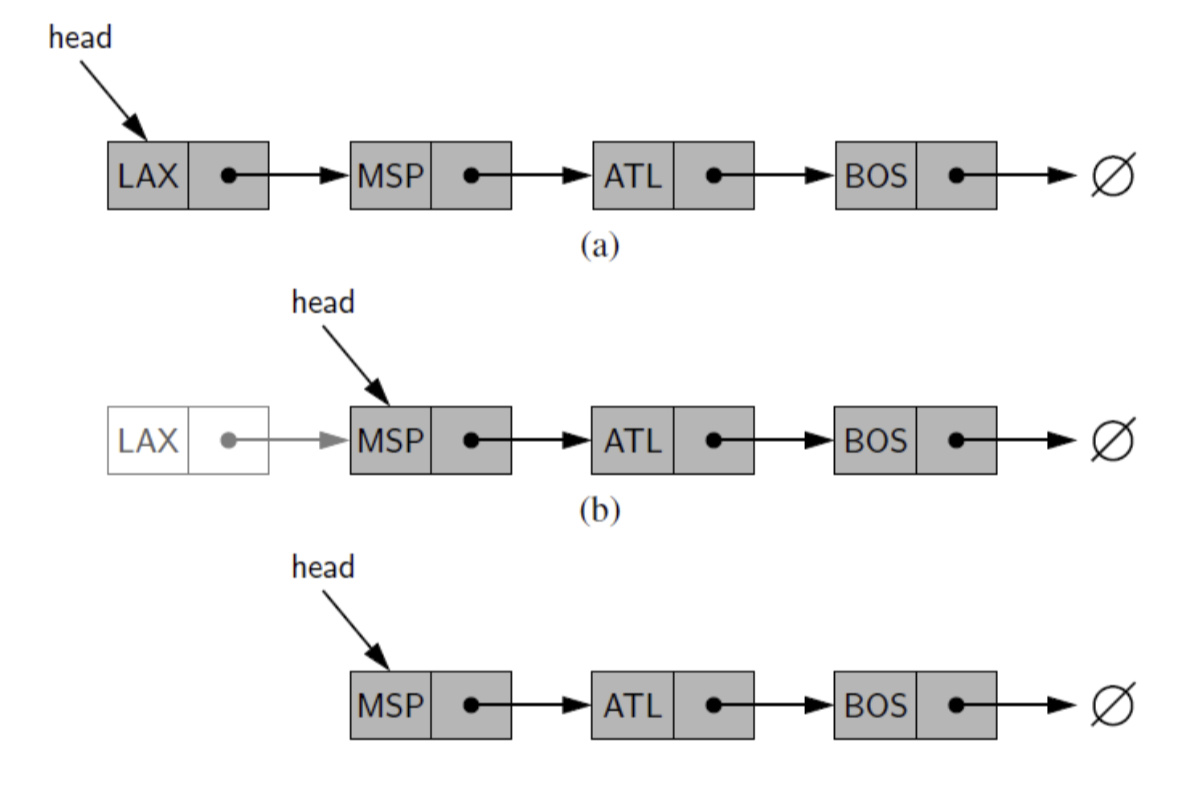
6) Removing an Element from the head

被移去的node仍旧存在在内存中，但已经不在链表中，python会自动删除这些数据

7) code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Node:
    def __init__(self,element,pointer):
        self.element = element
        self.pointer = pointer

class LinkedList:

    def __init__(self):
        self.head = None
        self.tail = None
        self.size = 0

    def add_first(self,e):
        newest = Node(e,None)
        newest.pointer = self.head
        self.head = newest
        self.size = self.size+1

        if self.size == 1:
            self.tail = newest

    def add_last(self,e):
        newest = Node(e,None)
        self.tail.pointer = newest
        self.tail = newest
        self.size = self.size+1

    def remove_first(self):
        if self.size == 0:
            print('The linked list is empty')
        else:
            self.head = self.head.pointer
            self.size = self.size - 1

8) Practice

  1. Implement stack with a singly linked list

之前的stack是用python的list实现，现在用链表实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class LinkedStack:
   
   def __init__(self):
       self.head = None
       self.size = 0

   def __len__(self):
       return self.size

   def is_empty(self):
       return self.size == 0

   def push(self,e):
       self.head = Node(e,self.head)
       self.size+=1

   def top(self):
       if self.is_empty():
           print('Stack is empty')
       else:
           return self.head.element

   def pop(self):
       if self.is_empty():
           print('Stack is empty')
       else:
           answer = self.head.element
           self.head = self.head.pointer
           self.size-=1
           return answer
  1. Implement queue with a singly linked list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class LinkedQueue:

   def __init__(self):
       self.head = None
       self.tail = None
       self.size = 0

   def __len__(self):
       return self.size

   def is_empty(self):
       return self.size == 0

   def first(self):
       if self.is_empty():
           print('Queue is empty')
       else:
           return self.head.element

   def dequeue(self):
       if self.is_empty():
           print('Queue is empty')
       else:
           answer = self.head.element
           self.head = self.head.pointer
           self.size-=1
           if self.is_empty():
               self.tail = None
           return answer

   def enqueue(self,e):
       newest = Node(e,None)

       if self.is_empty():
           self.head = newest
       else:
           self.tail.pointer = newest
       self.tail = newest
       self.size+=1

2.4 Circularly Linked List 循环链表

  • The tail of a linked list can use its next reference to point back to the head of the list
  • Such a structure is usually called a circularly linked list

无需储存head，因为head=tail.pointer

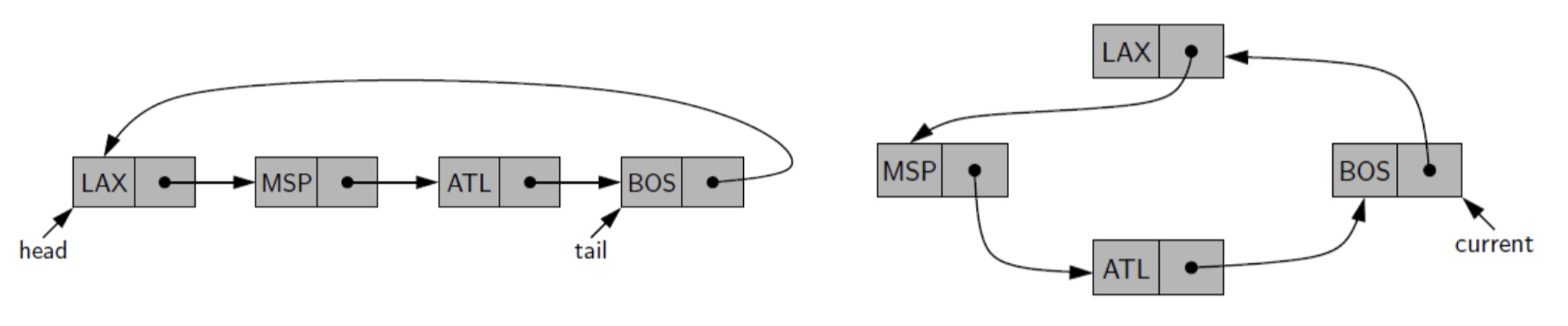
1) Example: Round-robin scheduler 循环调度

multi-tasking

一个处理器在某一时刻只会给一件任务提供服务，把时间分成很小的无数份，在不同的很小的时间内循环执行不同的程序

  • A round-robin scheduler iterates through a collection of elements in a circular fashion and “serves” each element by performing a given action on it
  • Such a scheduler is used, for example, to fairly allocate a resource that must be shared by a collection of clients
  • For instance, round-robin scheduling is often used to allocate slices of CPU time to various applications running concurrently on a computer

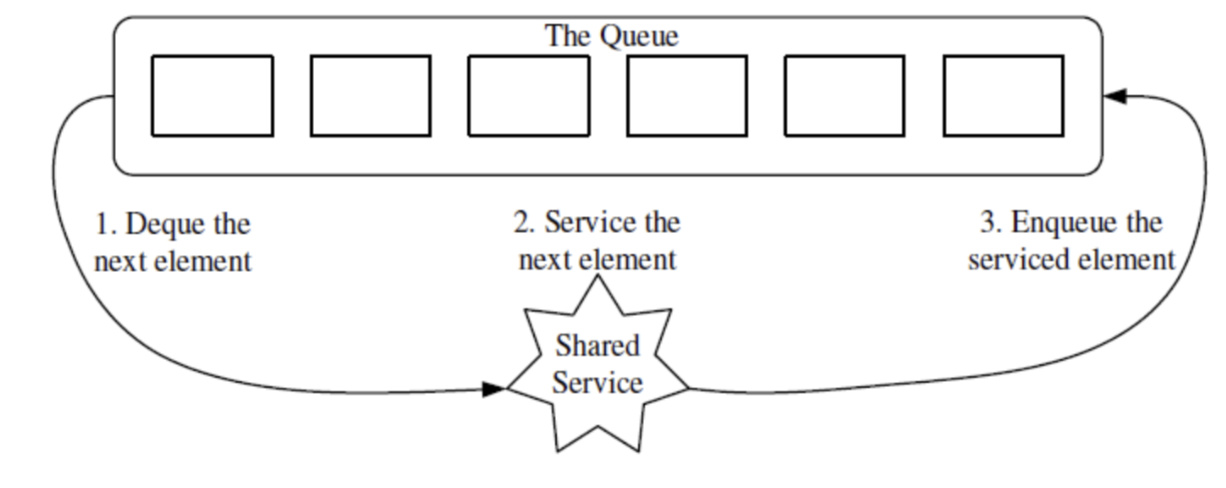
2) Implementing round-robin scheduler using standard queue

• A round-robin scheduler could be implemented with the standard queue, by repeatedly performing the following steps on queue Q:

  1. e = Q.dequeue()
  2. Service element e
  3. Q.enqueue(e)

3) Implement a Queue with a Circularly Linked List

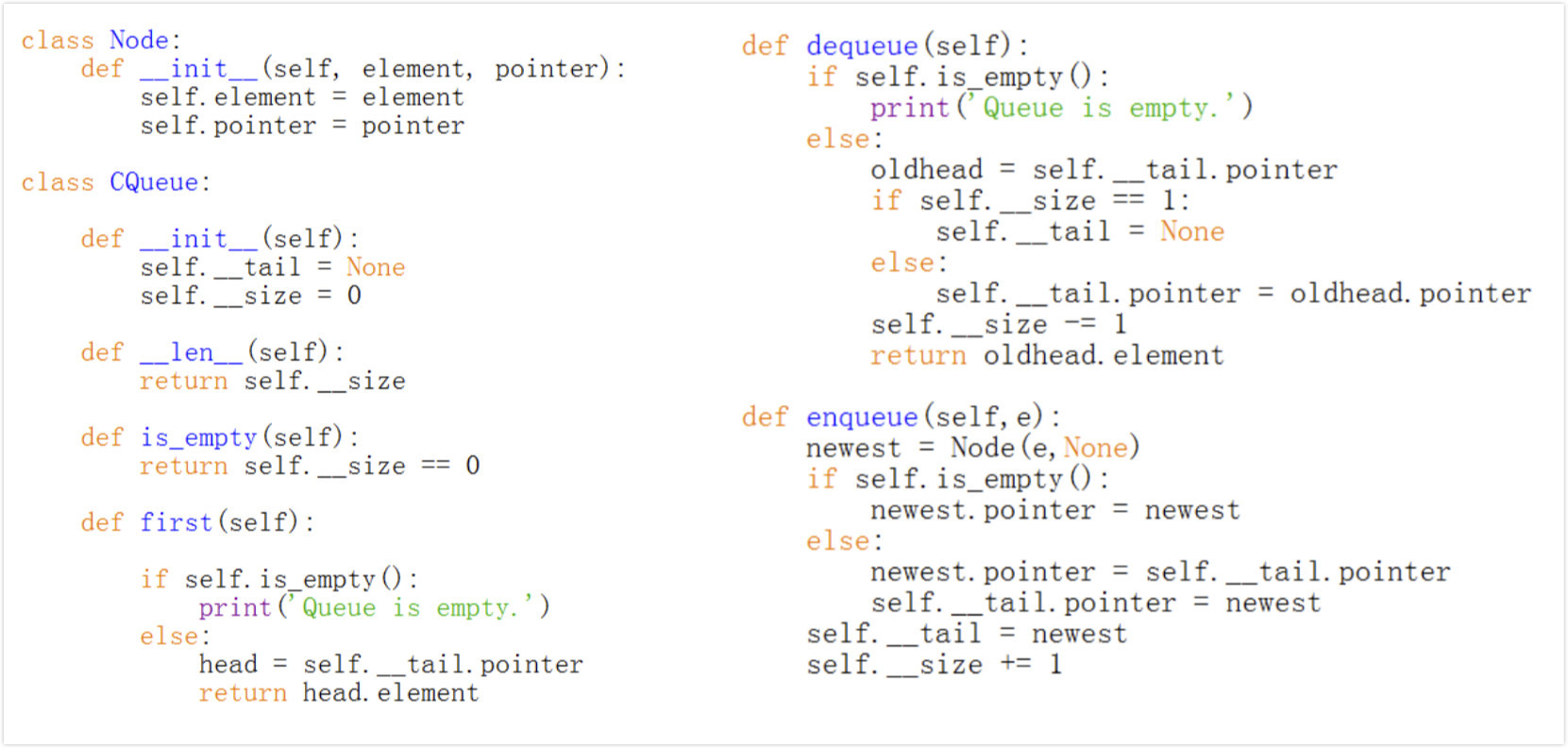
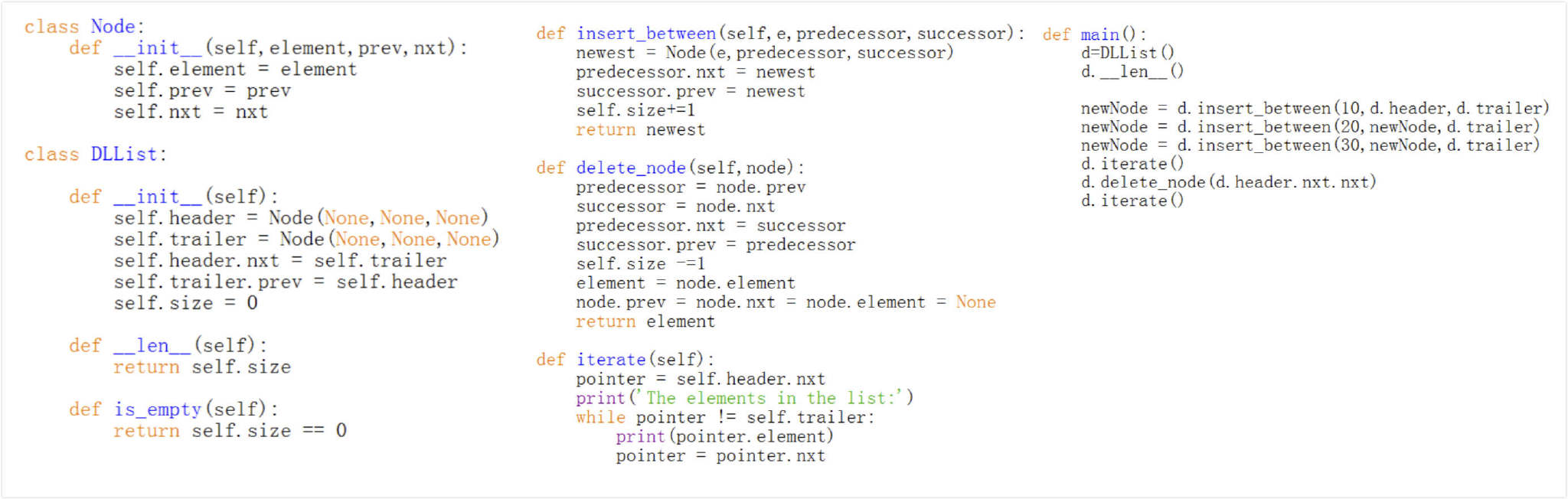
2.5 Doubly linked list 双链表

  • For a singly linked list, we can efficiently insert a node at either end of a singly linked list, and can delete a node at the head of a list
  • But we cannot efficiently delete a node at the tail of the list

普通的链表删除尾部的 node 的时间复杂度为 o(n)，因为要把倒数第二个的指针指向空，而只有往后的指针，没有往前的指针，所以要从头开始才能找到倒数第二个 node。

  • We can define a linked list in which each node keeps an explicit
    reference to the node before it and a reference to the node after it

从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点

  • In order to avoid some special cases when operating near the boundaries of a doubly linked list, it helps to add special nodes at
    both ends of the list: a header node at the beginning of the list, and a trailer node at the end of the list
  • These “dummy” nodes are known as sentinels (or guards), and they do not store elements of the primary sequence

Code

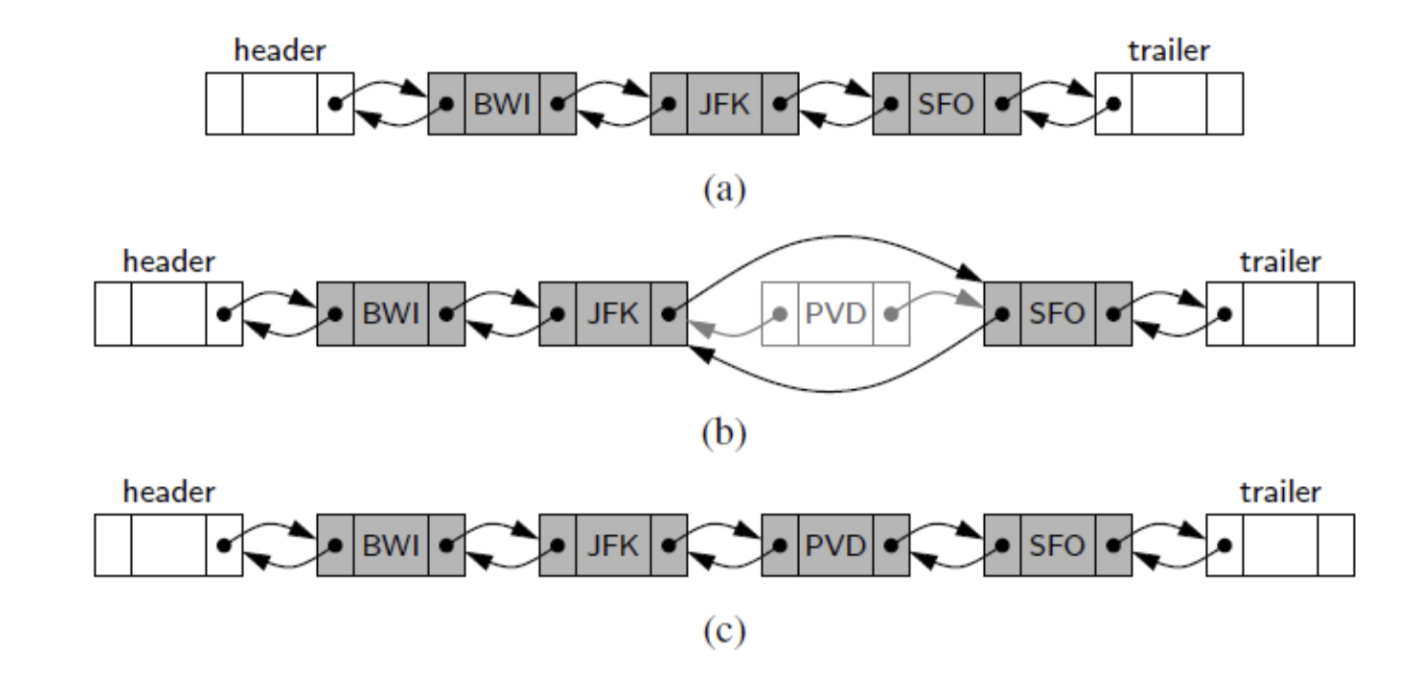
1) Inserting in the middle of a doubly linked list

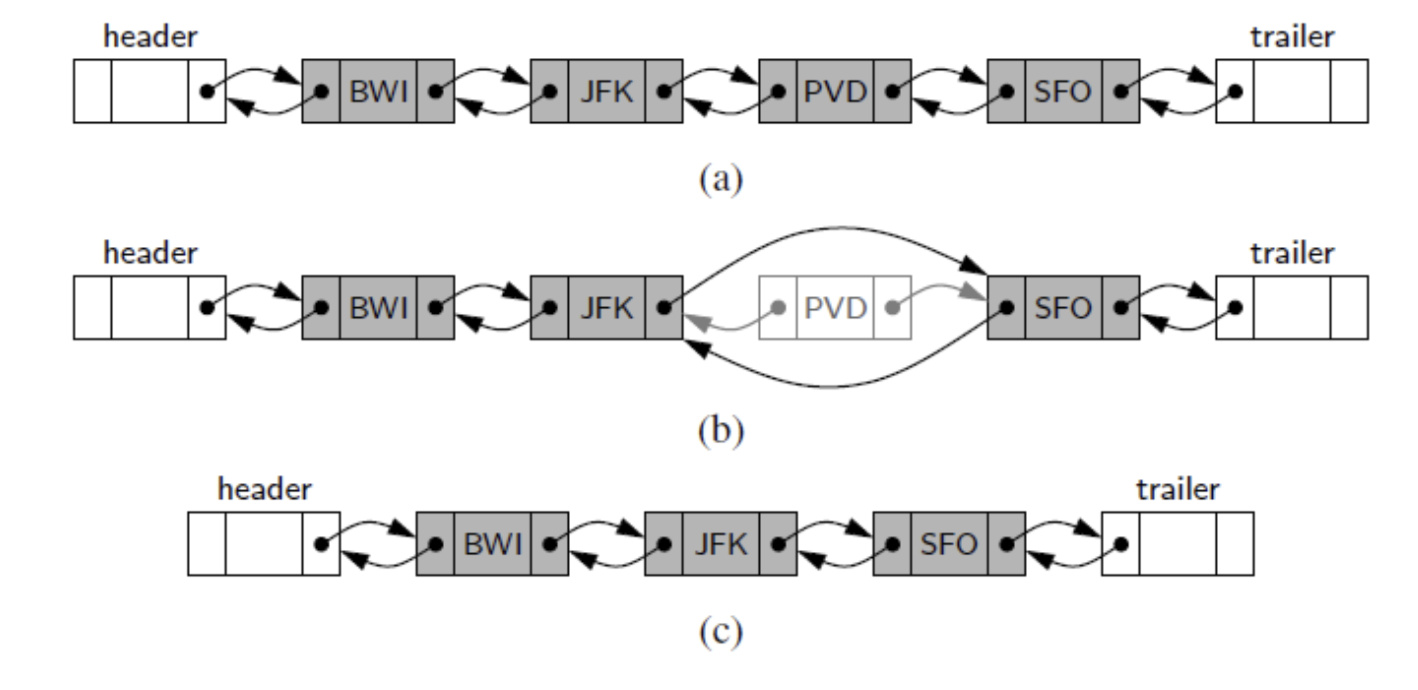
2) Deleting from the doubly linked list

2.6 Tree 树

  • A tree is a data structure that stores elements hierarchically（分层的）
  • With the exception of the top element, each element in a tree has a parent element and zero or more children elements
  • We typically call the top element the root of the tree（根节点）, but it is drawn as the highest element

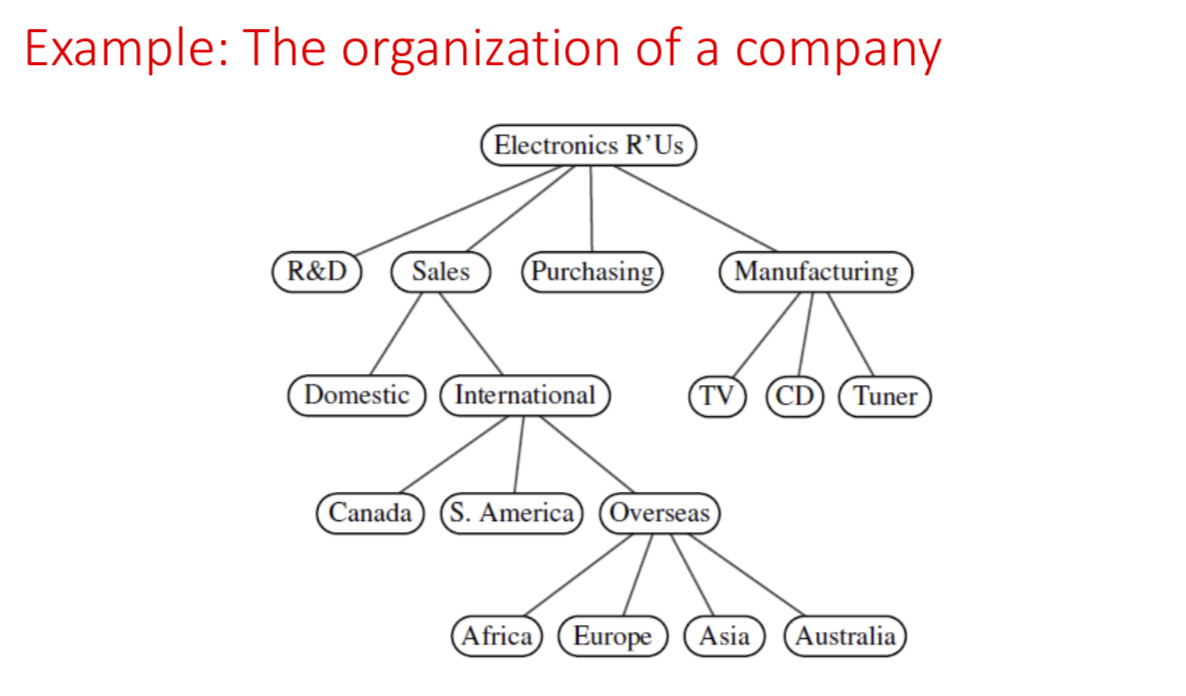
1) Edge 边 and path 路径

  • An edge 边 of tree T is a pair of nodes (u,v) such that u is the parent of v, or vice versa
  • A path 路径 of T is a sequence of nodes such that any two consecutive nodes in the sequence form an edge
  • The depth 深度 of a node v is the length of the path connecting root node and v（不包括自己）
  • leaf node 叶节点
  • internal node 内部节点

2) Ordered tree

A tree is ordered if there is a meaningful linear order among the children of each node（树中每个结点的各子树看成是从左到右有次序的）; such an order is usually visualized by arranging siblings from left to right, according to their order （之前公司的结构就是 Unordered Tree）

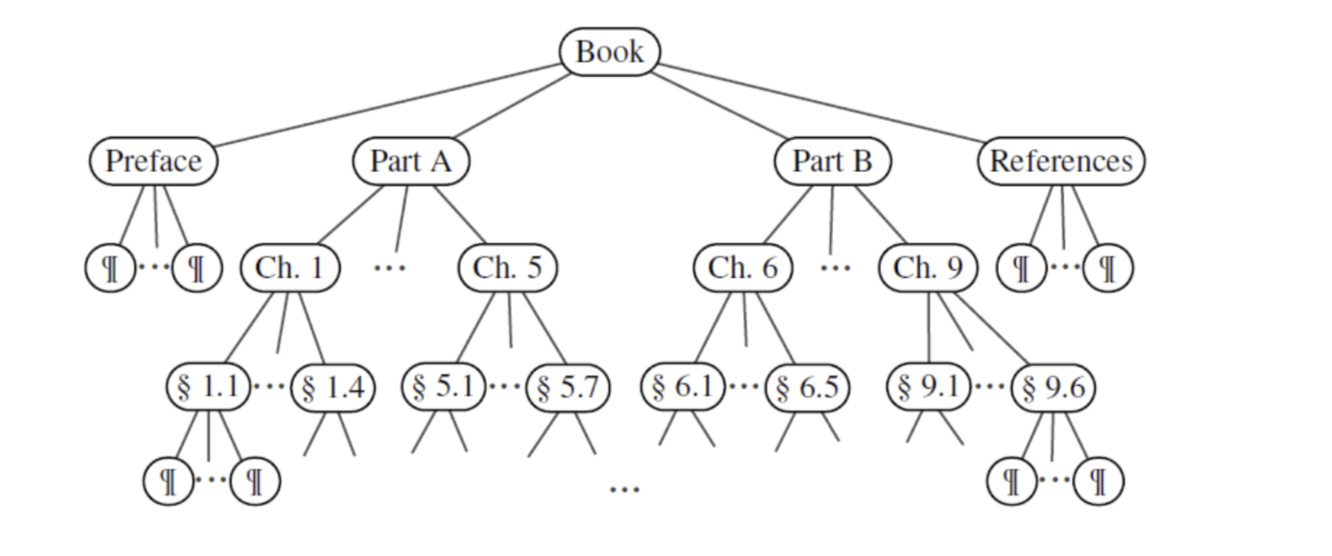
3) Binary tree

A binary tree is an ordered tree with the following properties:

  1. Every node has at most two children
  2. Each child node is labeled as being either a left child or a right child
  3. A left child precedes a right child in the order of children of a node

The subtree rooted at a left or right child of an internal node v is called a left subtree or right subtree, respectively, of v

A binary tree is proper if each node has either zero or two children（要不没有，要不2个）. Some people also refer to such trees as being full binary trees

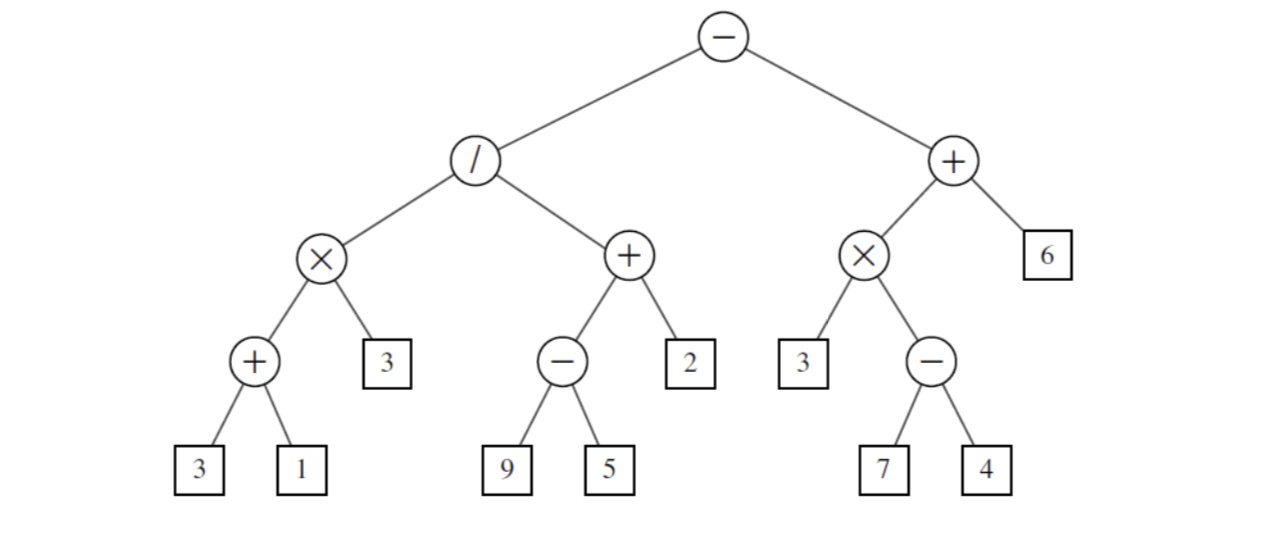
4) Example: Represent an expression with binary tree

An arithmetic expression（算术表达式）can be represented by a binary tree whose leaves are associated with variables or constants, and whose internal nodes are associated with one of the operators +, −, ×, and /

5) Binary tree class

  • We define a tree class based on a class called Node; an element is stored as a node

  • Each node contains 3 references（像是四个格子，第一个是数据）

    1. one pointing to the parent node,
    2. two pointing to the child nodes

6) Implementing the binary tree

7) Depth first search (DFS) 深度优先搜索算法

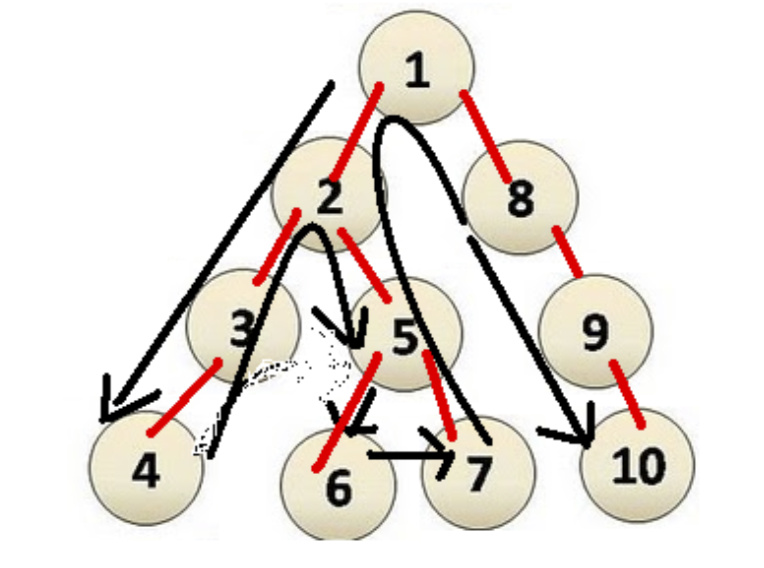
8) Breadth first search 广度优先搜索

Starts at the root and we visit all the positions at depth d before we visit the positions at depth d +1

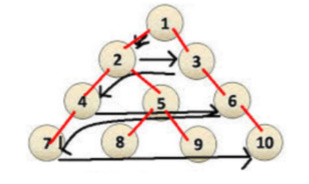
Example: finding the best strategy in a game

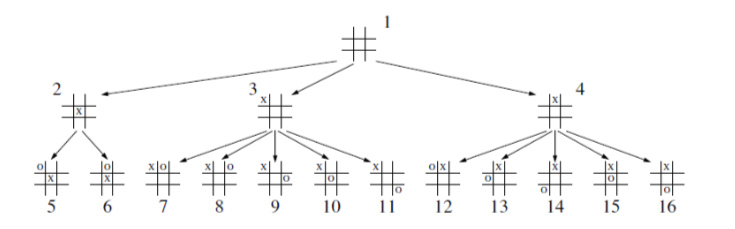
Code