卷积神经网络基础知识点
Padding
如果我们有一个 \(n × n\) 的图像,用 \(f × f\) 的过滤 器做卷积,那么输出的维度就是 \((n − f + 1) × (n − f + 1)\) 。
如果你用一个 \(3×3\) 的过滤器卷积一个 \(6×6\) 的图像,你最后会得 到一个 \(4×4\) 的输出,也就是一个 \(4×4\) 矩阵。那是因为你的 \(3×3\) 过滤器在 \(6×6\) 矩阵中,只可能有 \(4×4\) 种可能的位置
习惯上,你可以用 0 去填充,如果 \(p\) 是填充的数量,输出也就变成了 \((n + 2p − f + 1) × (n + 2p − f + 1)\)
这样一来,丢失信息或者更准确来说角落或图像边缘的信息发挥的作用较小的这一缺点就被削弱了。
沿着图像边缘再填充一层像素,那么 6×6 的图像就被填充成了一个 8×8 的图像。如果你用 3×3 的图像对这个 8×8 的图像卷积,你得到的输出就不是 4×4 的,而是 6×6 的图像,得到了一个尺寸和原始图像 6×6 的图像
至于选择填充多少像素,通常有两个选择,分别叫做 Valid 卷积和 Same 卷积:
Valid卷积意味着不填充,这样的话,如果你有一个 \(n × n\) 的图像,用一个 \(f × f\) 的过滤器 卷积,它将会给你一个 \((n − f + 1) × (n − f + 1)\) 维的输出。- 另一个经常被用到的填充方法叫做
Same卷积,那意味你填充后,你的输出大小和输入 大小是一样的。让 \(𝑛 + 2𝑝 − 𝑓 + 1 = 𝑛\) 的话,使得输 出和输入大小相等,如果你用这个等式求解 \(p\) ,那么 \(p =\frac {𝑓 − 1}{2}\) ,所以当 \(f\) 是一个奇数的时候,只要选择相应的填充尺寸,你就能确保得到和输入相同尺寸的输出。
为什么用奇数维过滤器?
只有 \(f\) 是奇数的 情况下,
Same卷积才会有自然的填充,我们可以以同样的数量填充四周,而不是左边填充多一点,右边填充少一点,这样不对称的填充。第二个原因是当你有一个奇数维过滤器,比如 3×3 或者 5×5 的,它就有一个中心点。有 时在计算机视觉里,如果有一个中心像素点会更方便,便于指出过滤器的位置。
Strided convolutions
如果你用一个 \(𝑓 × 𝑓\) 的过滤器卷积一个 \(𝑓 × 𝑓\) 的图像, 你的 padding 为 \(p\) ,步幅为 \(s\) ,现在不是一次移动一个步子,而是一次移动 \(s\) 个步子,输出于是变为 \(({\frac {n+2p-f}{s}+1})×({\frac {n+2p-f}{s}+1})\)
如果商不是一个整数怎么办?在这种情况下,我们向下 取整。⌊ ⌋ 这是向下取整的符号,这也叫做对 𝑧 进行地板除(floor),这意味着 𝑧 向下取整到最近的整数。
这个原则实现的方式是,只在蓝框完全包括在图像或填充完的图像内部时,才对它进行运算。如果有任意一个蓝框移动到了外面,那你就不要进行相乘操作,这是一个惯例。
总的来说: \(⌊{\frac {n+2p-f}{s}+1}⌋×⌊{\frac {n+2p-f}{s}+1}⌋\)
多维卷积
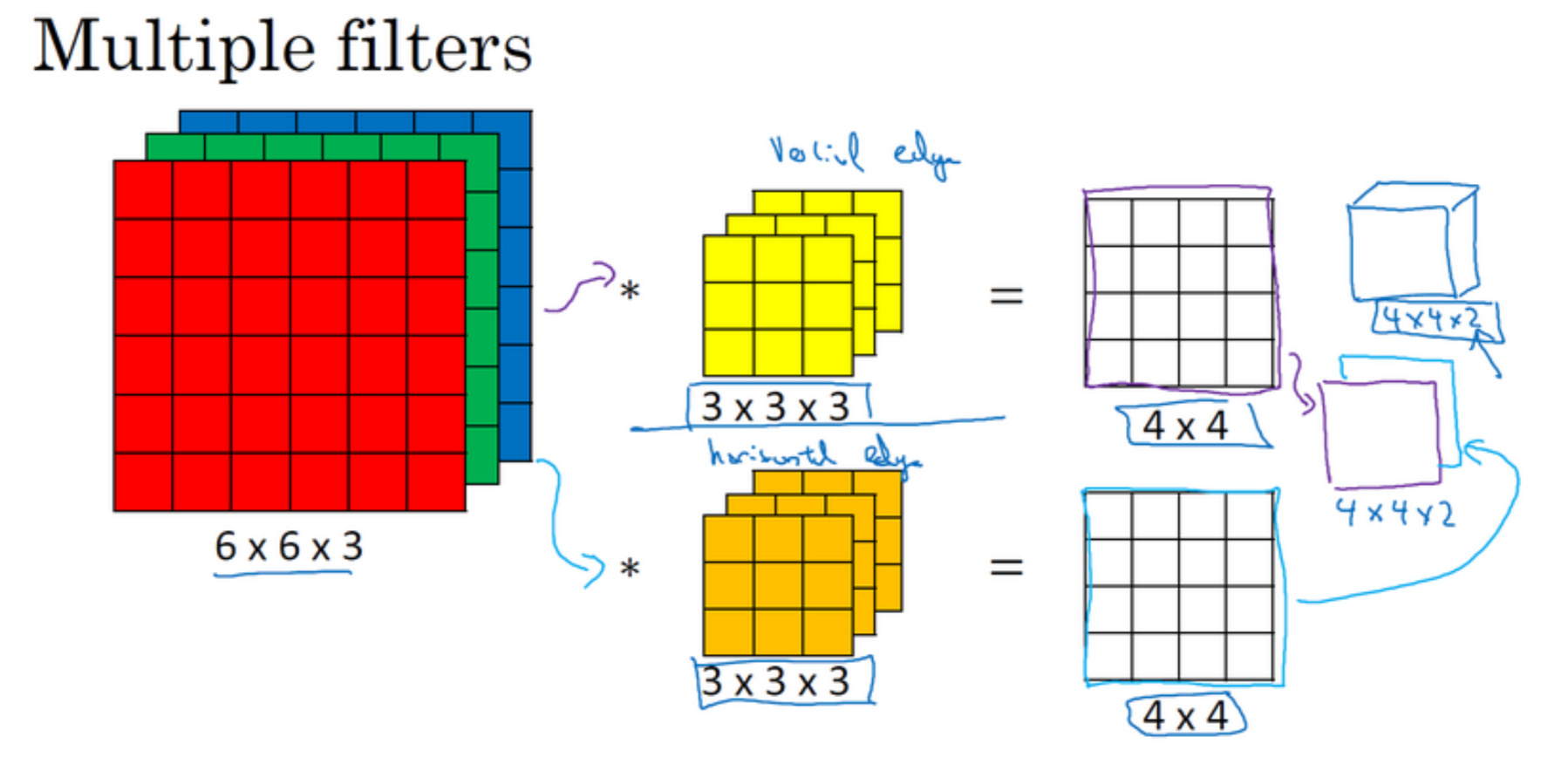
池化层
如果输入是三维的,那么输出也是三维的, \(n_c\) 个通道中每个通道都单独执行最大池化计算。
池化的超级参数包括过滤器大小𝑓和步幅𝑠,常用的参数值为 \(𝑓 = 2,𝑠 = 2\) , 应用频率非常高,其效果相当于高度和宽度缩减一半。也有使用 \(𝑓 = 3,𝑠 = 2\) 的情况。
最大池化时,往往很少用到超参数 padding,当 然也有例外的情况。
大部分情况下,最大池化很少用 padding。目前 \(𝑝\) 最常用
的值是 0,即 \(p=0\) 。最大池化的输入就是 \(𝑛_𝐻 × 𝑛_𝑊 × 𝑛_𝑐\) ,假设没有 padding,则输出 \(⌊\frac {𝑛_𝑤−𝑓}{s} + 1⌋ × ⌊\frac {𝑛_𝑤−𝑓}{s} + 1⌋ × 𝑛_𝑐 \) 。
输入通道与输出通道个数相同,因为我们对每个通道都做了池化。需 𝑠
要注意的一点是,池化过程中没有需要学习的参数。执行反向传播时,反向传播没有参数适用于最大池化。
1 × 1 卷积
\(1×1\) 的卷积能做什么呢?不就是乘以数字么?听上去挺好笑的,结果并非如此。
对于单通道的图片来说, \(1×1\) 卷积的确是把数字乘以一个数,效果不佳。
对于多通道的图片,使用\(1×1\) 卷积效果会更好。具体来说,\(1×1\) 卷积所实现的功能是遍历这 \(n_c\)(通道数) 个单元格,计算每一格中 \(n_c\) 个数字的元素积之和,然后应用 ReLU 非线性函数。
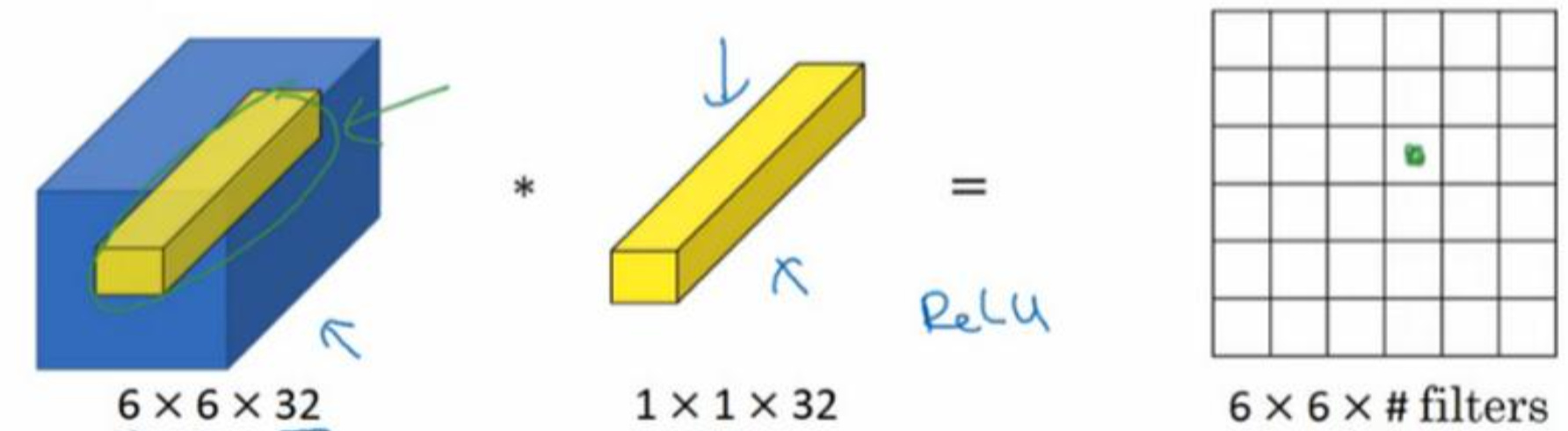
举个 \(1×1\) 卷积的例子
假设一个 \(28×28×192\) 的输入层,你可以使用池化层压缩它的高度和宽度。但如果通道数量很大,该如何把它压缩为 \(28×28×32\) 维度的层呢?
你可以用 \(32\) 个大小为 \(1×1\) 的过滤器,严格来讲每个过滤器大小都是 \(1×1×192\) 维,因为过滤器中通道数量 必须与输入层中通道的数量保持一致。但是你使用了 \(32\) 个过滤器,输出层为 \(28×28×32\)
这就是压缩通道数( \(𝑛_𝑐\) )的方法,对于池化层我只是压缩了这些层的高度和宽度。
当然如果 你想保持通道数 192 不变,这也是可行的,1×1 卷积只是添加了非线性函数,从而减少或保持输入层中的通道数量不变